【题目】甲、乙两车沿相同路线以各自的速度从A地去往B地,如图表示其行驶过程中路程y(千米)随时间t(小时)的变化图象,下列说法:

①乙车比甲车先出发2小时;
②乙车速度为40千米/时;
③A、B两地相距200千米;
④甲车出发80分钟追上乙车.
其中正确的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
参考答案:
【答案】D
【解析】①乙车比甲车先出发2小时,正确;
②乙车速度为80÷2=40千米/时,正确;
③A. B两地相距40×5=200千米,正确;
④甲的速度为200÷2=100千米/小时,
设甲车出发x分钟追上乙车,可得:100x=40(x+2)
解得:x=![]() ,
, ![]() 小时=80分钟,故正确,
小时=80分钟,故正确,
故选D.
点睛:本题考查了一次函数的应用, 观察图象,该函数图象表示的是路程与时间之间的函数关系,可知乙出发2小时后甲再出发,根据路程除以时间等于速度进行分析.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中,点(2,1)关于x轴的对称点是( )
A.(-2,1)
B.(-2,-1)
C.(2,-1)
D.(1,2) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,直线
 交
交 轴于点A,交
轴于点A,交 轴于点C(0,4).抛物线
轴于点C(0,4).抛物线
经过点A,交
 轴于点B(0,-2).点P为抛物线上一个动点,经过点P作
轴于点B(0,-2).点P为抛物线上一个动点,经过点P作 轴的垂线PD,过点B作BD⊥PD于点D,连接PB,设点P的横坐标为
轴的垂线PD,过点B作BD⊥PD于点D,连接PB,设点P的横坐标为 .
.(1)求抛物线的解析式;
(2)当△BDP为等腰直角三角形时,求线段PD的长;
(3)如图2,将△BDP绕点B逆时针旋转,得到△BD′P′,且旋转角∠PBP′=∠OAC,当点P的对应点P′落在坐标轴上时,请直接写出点P的坐标.



-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,D为AB上一点,△ACE≌△BCD,AD2+DB2=DE2,试判断△ABC的形状,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)观察与归纳:在如图1所示的平面直角坐标系中,直线l与y轴平行,点M与点N 是直线l上的两点(点M在点N的上方).
①亮亮发现:若点M坐标为(2,3),点N坐标为(2,﹣4),则MN的长度为_____; ②亮亮经过多次取l上的两点后,他归纳出这样的结论:若点M坐标为(t,m),点N坐标为(t,n),当m>n时,MN的长度可表示为______;
(2)如图2,四边形OABC的顶点O是坐标原点,点A在第一象限,
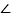 OAB=90
OAB=90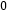 ,OA=AB,点C在第四象限,B点的坐标为(6,0),且OC=5.点P是线段OB上的一个动点(点P不与点0、B重合),过点P作与y轴平行的直线l,设点P横坐标为t.
,OA=AB,点C在第四象限,B点的坐标为(6,0),且OC=5.点P是线段OB上的一个动点(点P不与点0、B重合),过点P作与y轴平行的直线l,设点P横坐标为t.①已知当t=4时,直线l恰好经过点C,求点A、C两点的坐标;
②在①的条件下,直线l上有一点M,当MB=
 OC时,直接写出满足条件的点M坐标;
OC时,直接写出满足条件的点M坐标;③如图3延长线段BA交y轴于点D将线段BD顺时针旋转60
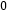 ,D点的对应点为点E,是否存 在x轴上的点Q,使得QD+QE的值最小,若存在请求出点Q的坐标,并求出
,D点的对应点为点E,是否存 在x轴上的点Q,使得QD+QE的值最小,若存在请求出点Q的坐标,并求出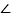 OQD的度数; 若不存在,请说明理由.
OQD的度数; 若不存在,请说明理由.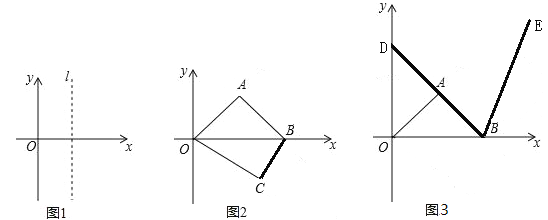
-
科目: 来源: 题型:
查看答案和解析>>【题目】若等腰三角形有两条边的长度为2和5,则此等腰三角形的周长为( )
A. 9 B. 12 C. 9或12 D. 10
-
科目: 来源: 题型:
查看答案和解析>>【题目】用代数式表示“a的3倍与b的平方的差”,正确的是( )
A. (3a﹣b)2 B. 3(a﹣b)2 C. (a﹣3b)2 D. 3a﹣b2
相关试题

