搜索
【题目】如图，MN是半径为2的⊙O的直径，点A在⊙O上，∠AMN＝30°，点B为劣弧AN的中点．点P是直径MN上一动点，则PA＋PB的最小值为( )
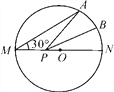
A. 4
B. 2 C. 4 D. 2
参考答案：
【答案】D
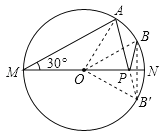
【解析】解：作点B关于MN的对称点B′，连接OA、OB、OB′、AB′，则AB′与MN的交点即为PA+PB的最小时的点，PA+PB的最小值=AB′．∵∠AMN=30°，∴∠AON=2∠AMN=2×30°=60°．∵点B为劣弧AN的中点，∴∠BON=
∠AON=×60°=30°，由对称性，∠B′ON=∠BON=30°，∴∠AOB′=∠AON+∠B′ON=60°+30°=90°，∴△AOB′是等腰直角三角形，∴AB′=
OA=×2=
，即PA+PB的最小值=．故选D．
-
科目： 来源： 题型：
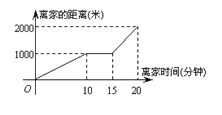
查看答案和解析>>【题目】某天小明骑自行车上学，途中因自行车发生故障，修车耽误了一段时间后继续骑行，按时赶到了学校，如图所示是小明从家到学校这一过程中所走的路程 s（米）与时间 t（分）之间的关系．
（1）小明从家到学校的路程共 米，从家出发到学校，小明共用了 分钟；
（2）小明修车用了多长时间？
（3）小明修车以前和修车后的平均速度分别是多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在正方形ABCD中，E是BC上的一点，连接AE，作BF⊥AE，垂足为H，交CD于F，作CG∥AE，交BF于G．
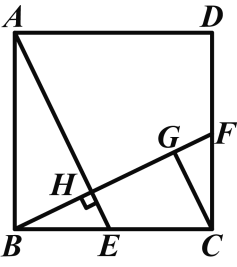
求证：（1）CG＝BH；
（2）FC2＝BF·GF；
（3）
． -
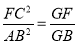科目： 来源： 题型：
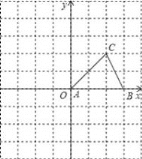
查看答案和解析>>【题目】如图,△ABC的顶点A在原点,B、C坐标分别为B(3,0),C(2,2),将△ABC向左平移1个单位后再向下平移2单位,可得到△A′B′C′.
(1)请画出平移后的△A′B′C′的图形；
(2)写出△A′B′C′各个顶点的坐标；
(3)求△ABC的面积.
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知在以点O为圆心的两个同心圆中，大圆的弦AB交小圆于点C、D(如图)．
(1)求证：AC＝BD；
(2)若大圆的半径R＝10，小圆的半径r＝8，且圆心O到直线AB的距离为6，求AC的长．
-
科目： 来源： 题型：
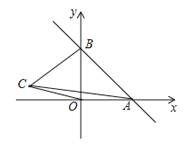
查看答案和解析>>【题目】如图，一次函数y=kx+b的图象分别与x轴，y轴的正半轴分別交于点A，B，AB=2
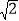，∠OAB=45°（1）求一次函数的解析式；
（2）如果在第二象限内有一点C(a，
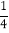)；试用含有a的代数式表示四边形ABCO的面积，并求出当△ABC的面积与△ABO的面积相等时a的值； （3）在x轴上，是否存在点P，使△PAB为等腰三角形？若存在，请直接写出所有符合条件的点P坐标；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知∠1＝∠2，要说明△ABD≌△ACD，还需从下列条件中选一个，错误的选法是（ ）
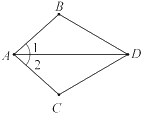
A. ∠ADB＝∠ADCB. ∠B＝∠CC. DB＝DCD. AB＝AC
相关试题
