【题目】某乡镇实施产业扶贫,帮助贫困户承包了荒山种植蜜柚,已知该蜜柚的成本价为8元/千克。
到了收获季节,投入市场销售时,调查市场行情,发现该蜜柚销售不会亏本,且每天销量
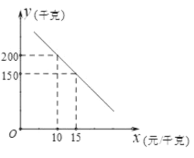
干克)与销售单价x(元/千克)之间的函数关系如图所示.
(1)求y与x的函数关系式,并写出x的取值范围:
(2)当该蜜柚定价为多少时,每天销售获得的利润最大?最大利润是多少?
(3)某农户今年共采摘蜜柚4800千克,该蜜柚的保持期为40天,根据(2)中获得最大利润的方式进行销售,能否销售完这批蜜柚?请说明理由.
参考答案:
【答案】(1)y与x的函数关系式为y=-10x+300(8≤x≤30);(2)x=19时,w取得最大值,最大值为1210;(3)不能销售完这批蜜柚.
【解析】
(1)利用待定系数法求解可得;
(2)根据“总利润=单件利润×销售量”列出函数解析式,并配方成顶点式即可得出最大值;
(3)求出在(2)中情况下,即x=19时的销售量,据此求得40天的总销售量,比较即可得出答案.
(1)设y与x的函数关系式为y=kx+b,
将(10,200)、(15,150)代入,得:![]() ,
,
解得:![]() ,
,
∴y与x的函数关系式为y=-10x+300(8≤x≤30);
(2)设每天销售获得的利润为w,
则w=(x-8)y
=(x-8)(-10x+300)
=-10(x-19)2+1210,
∵8≤x≤30,
∴当x=19时,w取得最大值,最大值为1210;
(3)由(2)知,当获得最大利润时,定价为19元/千克,
则每天的销售量为y=-10×19+300=110千克,
∵保质期为40天,
∴总销售量为40×110=4400,
又∵4400<4800,
∴不能销售完这批蜜柚.
-
科目: 来源: 题型:
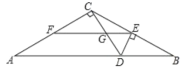
查看答案和解析>>【题目】如图,已知EF是△ABC的中位线,DE⊥BC交AB于点D,CD与EF交于点G,若CD⊥AC,EF=8,EG=3,则AC的长为___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,边长为a的正方形发生形变后成为边长为a的菱形,如果这个菱形的一组对边之间的距离为h,我们把
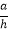 的值叫做这个菱形的“形变度”.例如,当形变后的菱形是如图2形状(被对角线BD分成2个等边三角形),则这个菱形的“形变度”为2:
的值叫做这个菱形的“形变度”.例如,当形变后的菱形是如图2形状(被对角线BD分成2个等边三角形),则这个菱形的“形变度”为2: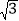 .如图3,正方形由16个边长为1的小正方形组成,形变后成为菱形,△AEF(A、E、F是格点)同时形变为△A′E′F′,若这个菱形的“形变度”k=
.如图3,正方形由16个边长为1的小正方形组成,形变后成为菱形,△AEF(A、E、F是格点)同时形变为△A′E′F′,若这个菱形的“形变度”k=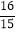 ,则S△A′E′F′=__
,则S△A′E′F′=__
-
科目: 来源: 题型:
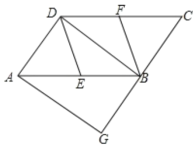
查看答案和解析>>【题目】如图,在平行四边形ABCD中,E、 F分别为边AB、CD的中点,BD是对角线.过点有作AG∥DB交CB的延长线于点G.
(1)求证:△ADE≌△CBF;
(2)若∠G=90° ,求证:四边形DEBF是菱形.
-
科目: 来源: 题型:
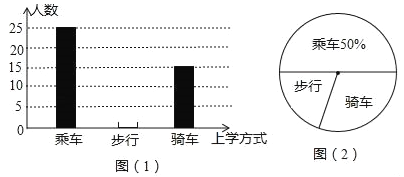
查看答案和解析>>【题目】学习了统计知识后,小明就本班同学的上学方式进行了一次调查统计.图(1)和图(2)是他通过采集数据后,绘制的两幅不完整的统计图.请你根据图中提供的信息,解答以下问题:
(1)求该班学生的人数;
(2)在图(1)中,将表示“步行”的部分补充完整;
(3)如果全年级共600名同学,请你估算全年级步行上学的学生人数?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点M是正方形ABCD的边BC上一点,连接AM,点E是线段AM上一点,∠CDE的平分线交AM延长线于点F.
(1)如图1,若点E为线段AM的中点,BM:CM=1:2,BE=
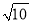 ,求AB的长;
,求AB的长;(2)如图2,若DA=DE,求证:BF+DF=
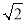 AF.
AF.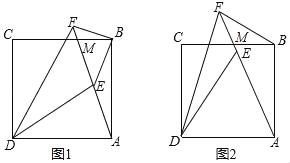
-
科目: 来源: 题型:
查看答案和解析>>【题目】代数式:①-x;②x2+x-1;③
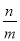 ;④
;④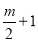 ;⑤
;⑤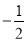 ;⑥πm3y;⑦
;⑥πm3y;⑦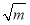 ;⑧
;⑧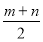 .
.(1)请上述代数式的序号分别填在相应的圆圈内:

(2)其中次数最高的多项式是__________次_________项式;
(3)其中次数最高的单项式的次数是____________,系数是____________.
相关试题

