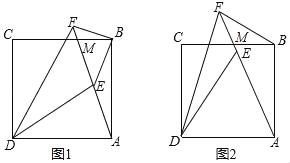
【题目】如图,点M是正方形ABCD的边BC上一点,连接AM,点E是线段AM上一点,∠CDE的平分线交AM延长线于点F.
(1)如图1,若点E为线段AM的中点,BM:CM=1:2,BE=![]() ,求AB的长;
,求AB的长;
(2)如图2,若DA=DE,求证:BF+DF=![]() AF.
AF.
参考答案:
【答案】(1)AB=6;(2)证明见解析.
【解析】
(1)设BM=x,则CM=2x,BC=BA=3x;在Rt△ABM中,E为斜边AM中点,根据直角三角形斜边的中线等于斜边的一半可得AM=2BE=2![]() .由勾股定理可得AM2=MB2+AB2,即可得40=x2+9x2,解得x=2.所以AB=3x=6;(2)延长FD交过点A作垂直于AF的直线于H点,过点D作DP⊥AF于P点.证明△ABF≌△ADH,根据全等三角形的性质可得AF=AH,BF=DH.再由Rt△FAH是等腰直角三角形,可得HF=
.由勾股定理可得AM2=MB2+AB2,即可得40=x2+9x2,解得x=2.所以AB=3x=6;(2)延长FD交过点A作垂直于AF的直线于H点,过点D作DP⊥AF于P点.证明△ABF≌△ADH,根据全等三角形的性质可得AF=AH,BF=DH.再由Rt△FAH是等腰直角三角形,可得HF=![]() AF.由HF=DH+DF=BF+DF,可得BF+DF=
AF.由HF=DH+DF=BF+DF,可得BF+DF=![]() AF.
AF.
解:(1)设BM=x,则CM=2x,BC=3x,
∵BA=BC,
∴BA=3x.
在Rt△ABM中,E为斜边AM中点,
∴AM=2BE=2![]() .
.
由勾股定理可得AM2=MB2+AB2,
即40=x2+9x2,解得x=2.
∴AB=3x=6.
(2)延长FD交过点A作垂直于AF的直线于H点,过点D作DP⊥AF于P点.
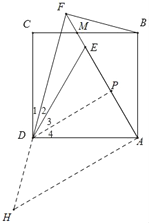
∵DF平分∠CDE,
∴∠1=∠2.
∵DE=DA,DP⊥AF
∴∠3=∠4.
∵∠1+∠2+∠3+∠4=90°,
∴∠2+∠3=45°.
∴∠DFP=90°﹣45°=45°.
∴AH=AF.
∵∠BAF+∠DAF=90°,∠HAD+∠DAF=90°,
∴∠BAF=∠DAH.
又AB=AD,
∴△ABF≌△ADH(SAS).
∴AF=AH,BF=DH.
∵Rt△FAH是等腰直角三角形,
∴HF=![]() AF.
AF.
∵HF=DH+DF=BF+DF,
∴BF+DF=![]() AF.
AF.
-
科目: 来源: 题型:
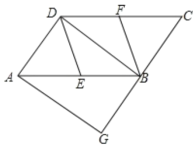
查看答案和解析>>【题目】如图,在平行四边形ABCD中,E、 F分别为边AB、CD的中点,BD是对角线.过点有作AG∥DB交CB的延长线于点G.
(1)求证:△ADE≌△CBF;
(2)若∠G=90° ,求证:四边形DEBF是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某乡镇实施产业扶贫,帮助贫困户承包了荒山种植蜜柚,已知该蜜柚的成本价为8元/千克。
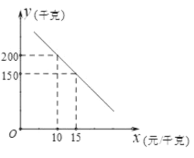
到了收获季节,投入市场销售时,调查市场行情,发现该蜜柚销售不会亏本,且每天销量
干克)与销售单价x(元/千克)之间的函数关系如图所示.
(1)求y与x的函数关系式,并写出x的取值范围:
(2)当该蜜柚定价为多少时,每天销售获得的利润最大?最大利润是多少?
(3)某农户今年共采摘蜜柚4800千克,该蜜柚的保持期为40天,根据(2)中获得最大利润的方式进行销售,能否销售完这批蜜柚?请说明理由.
-
科目: 来源: 题型:
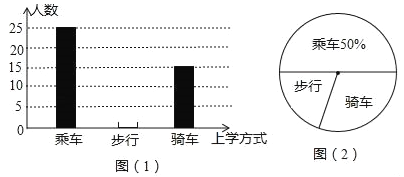
查看答案和解析>>【题目】学习了统计知识后,小明就本班同学的上学方式进行了一次调查统计.图(1)和图(2)是他通过采集数据后,绘制的两幅不完整的统计图.请你根据图中提供的信息,解答以下问题:
(1)求该班学生的人数;
(2)在图(1)中,将表示“步行”的部分补充完整;
(3)如果全年级共600名同学,请你估算全年级步行上学的学生人数?
-
科目: 来源: 题型:
查看答案和解析>>【题目】代数式:①-x;②x2+x-1;③
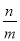 ;④
;④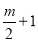 ;⑤
;⑤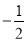 ;⑥πm3y;⑦
;⑥πm3y;⑦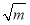 ;⑧
;⑧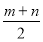 .
.(1)请上述代数式的序号分别填在相应的圆圈内:

(2)其中次数最高的多项式是__________次_________项式;
(3)其中次数最高的单项式的次数是____________,系数是____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=
 x+6的图象与x轴、y轴分别交于A、B两点,点C与点A关于y轴对称.动点P、Q分别在线段AC、AB上(点P与点A、C不重合),且满足∠BPQ=∠BAO。
x+6的图象与x轴、y轴分别交于A、B两点,点C与点A关于y轴对称.动点P、Q分别在线段AC、AB上(点P与点A、C不重合),且满足∠BPQ=∠BAO。(1)求点A、 B的坐标及线段BC的长度;
(2)当点P在什么位置时,△APQ≌△CBP,说明理由;
(3)当△PQB为等腰三角形时,求点P的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】点P,Q在数轴上分别表示的数分别为p,q,我们把p,q之差的绝对值叫做点P,Q之间的距离,即
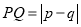 .如图,在数轴上,点A,B,O,C,D的位置如图所示,则
.如图,在数轴上,点A,B,O,C,D的位置如图所示,则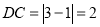 ;
; ;
;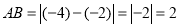 .请探索下列问题:
.请探索下列问题:
(1)计算
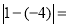 ____________,它表示哪两个点之间的距离?________________________.
____________,它表示哪两个点之间的距离?________________________.(2)点M为数轴上一点,它所表示的数为x,用含x的式子表示PB=____________;当PB=2时,x=____________;当x=____________时,|x+4|+|x-1|+|x-3|的值最小.
(3)|x-1|+|x-2|+|x-3|+…+|x-2018|+|x-2019|的最小值为________________________.
相关试题

