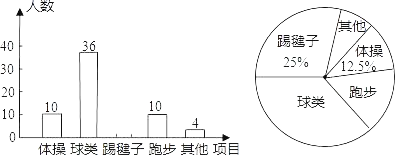
【题目】为了了解全校1800名学生对学校设置的体操、球类、跑步、踢毽子等课外体育活动项目的喜爱情况,在全校范围内随机抽取了若干名学生.对他们最喜爱的体育项目(每人只选一项)进行了问卷调查,将数据进行了统计并绘制成了如图所示的频数分布直方图和扇形统计图(均不完整).
(1)补全频数分布直方图;
(2)求扇形统计图中表示“踢毽子”项目扇形圆心角的度数.
(3)估计该校1800名学生中有多少人最喜爱球类活动?
参考答案:
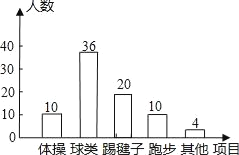
【答案】(1) 80名;(2) 20人,补全图形见解析;(3)估计全校有810人最喜欢球类活动.
【解析】
(1)根据参加体操的人数为10人,占扇形图的12.5%,即可得出参加活动的总人数,即可求出踢毽子的人数;
(2)根据踢毽子的人数所占的比例即可得出扇形圆心角的度数;
(3)根据样本估计总体,即可得出估计全校最喜欢球类活动的人数.
(1)10÷12.5%×25%=20(人),如图所示.
(2)扇形统计图中表示“踢毽子”项目扇形圆心角的度数为![]() =90°;
=90°;
(3)![]() (人).
(人).
估计全校有810人最喜欢球类活动.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx﹣2(a≠0)与x轴交于A、B两点,与y轴交于C点,直线BD交抛物线于点D,并且D(2,3),tan∠DBA=
 .
.(1)求抛物线的解析式;
(2)已知点M为抛物线上一动点,且在第三象限,顺次连接点B、M、C、A,求四边形BMCA面积的最大值;
(3)在(2)中四边形BMCA面积最大的条件下,过点M作直线平行于y轴,在这条直线上是否存在一个以Q点为圆心,OQ为半径且与直线AC相切的圆?若存在,求出圆心Q的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为6cm,动点P从A点出发,在正方形的边上由A→B→C→D运动,设运动的时间为t(s),△APD的面积为S(cm2),S与t的函数图象如图所示
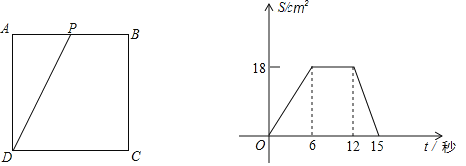
(1)求点P在BC上运动的时间范围;
(2)当t为何值时,△APD的面积为10cm2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】嘉淇乘坐一艘游船出海游玩,游船上的雷达扫描探测得到的结果如图所示,每相邻两个圆之间距离是1km (最小圆的半径是1km ),下列关于小艇 A , B 的位置描述,正确的是( )

A.小艇 A 在游船的北偏东60°方向上,且与游船的距离是3km
B.游船在小艇 A 的南偏西60°方向上,且与小艇 A 的距离是3km
C.小艇 B 在游船的北偏西30°方向上,且与游船的距离是 2km
D.游船在小艇 B 的南偏东60°方向上,且与小艇 B 的距离是 2km
-
科目: 来源: 题型:
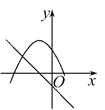
查看答案和解析>>【题目】在同一平面直角坐标系中,函数y=mx+m和函数y=-mx2+2x+2(m是常数,且m≠0)的图象可能是( )
A.
 B.
B. 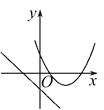 C.
C. 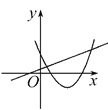 D.
D. 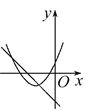
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 中,
中, ,D,E,F分别为AB,BC,CA上的点,且
,D,E,F分别为AB,BC,CA上的点,且 ,
, .
.(1)求证:
 ≌
≌ ;
;(2)若
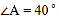 ,求
,求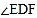 的度数.
的度数.
-
科目: 来源: 题型:
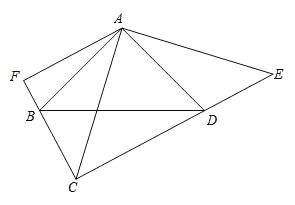
查看答案和解析>>【题目】如图, BAD CAE 90 , AB AD , AE AC , ABD ADB ACE AEC 45 ,AF CF ,垂足为 F .
(1)若 AC 10 ,求四边形 ABCD 的面积;
(2)求证: CE 2 AF .
相关试题

