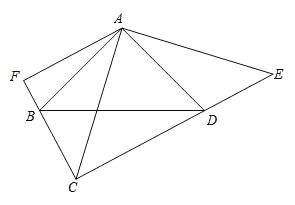
【题目】如图, BAD CAE 90 , AB AD , AE AC , ABD ADB ACE AEC 45 ,AF CF ,垂足为 F .
(1)若 AC 10 ,求四边形 ABCD 的面积;
(2)求证: CE 2 AF .
参考答案:
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)求出∠BAC=∠EAD,根据SAS推出△ABC≌△ADE,推出四边形ABCD的面积=三角形ACE的面积,即可得出答案;
(2)过点A作AG⊥CG,垂足为点G,求出AF=AG,求出CG=AG=GE,即可解决问题.
(1)解:∵∠BAD=∠CAE=90°,
∴∠BAC+∠CAD=∠EAD+∠CAD
∴∠BAC=∠EAD,
在△ABC和△ADE中,
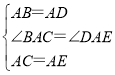 ,
,
∴△ABC≌△ADE(SAS),
∵S四边形ABCD=S△ABC+S△ACD,
∴S四边形ABCD=S△ADE+S△ACD=S△ACE=![]() ×102=50;
×102=50;
(2)证明:∵△ACE是等腰直角三角形,
∴∠ACE=∠AEC=45°,
由△ABC≌△ADE得:
∠ACB=∠AEC=45°,
∴∠ACB=∠ACE,
∴AC平分∠ECF;
过点A作AG⊥CG,垂足为点G,
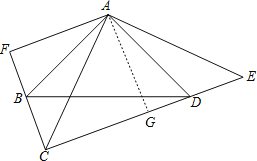
∵AC平分∠ECF,AF⊥CB,
∴AF=AG,
又∵AC=AE,
∴∠CAG=∠EAG=45°,
∴∠CAG=∠EAG=∠ACE=∠AEC=45°,
∴CG=AG=GE,
∴CE=2AG,
∴CE=2AF.
-
科目: 来源: 题型:
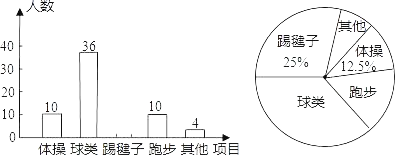
查看答案和解析>>【题目】为了了解全校1800名学生对学校设置的体操、球类、跑步、踢毽子等课外体育活动项目的喜爱情况,在全校范围内随机抽取了若干名学生.对他们最喜爱的体育项目(每人只选一项)进行了问卷调查,将数据进行了统计并绘制成了如图所示的频数分布直方图和扇形统计图(均不完整).
(1)补全频数分布直方图;
(2)求扇形统计图中表示“踢毽子”项目扇形圆心角的度数.
(3)估计该校1800名学生中有多少人最喜爱球类活动?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一平面直角坐标系中,函数y=mx+m和函数y=-mx2+2x+2(m是常数,且m≠0)的图象可能是( )
A.
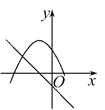 B.
B. 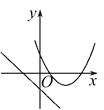 C.
C. 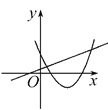 D.
D. 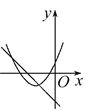
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 中,
中, ,D,E,F分别为AB,BC,CA上的点,且
,D,E,F分别为AB,BC,CA上的点,且 ,
, .
.(1)求证:
 ≌
≌ ;
;(2)若
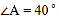 ,求
,求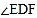 的度数.
的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=CB,延长DA与⊙O的另一个交点为E,连接AC,CE.
(1)求证:∠B=∠D;
(2)若AB=4,BC﹣AC=2,求CE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中每个小正方形的边长都是1个单位长度,Rt△ABC的三个顶点A(-2,2),B(0,5),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,得到△A1B1C,请画出△A1B1C的图形.
(2)平移△ABC,使点A的对应点A2坐标为(-2,-6),请画出平移后对应的△A2B2C2的图形.
(3)若将△A1B1C绕某一点旋转可得到△A2B2C2,请直接写出旋转中心的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】定义一种新运算“a*b”:当a≥b时,a*b=a+2b;当a<b时,a*b=a-2b.
例如:3*(-4)=3+(-8)=-5,(-6)*12=-6-24=-30
(1)填空:(-4)*3= .
(2)若(3x-4)*(x+6)=(3x-4)+2(x+6),则x的取值范围为 ;
(3)已知(3x-7)*(3-2x)<-6,求x的取值范围;
(4)小明在计算(2x2-4x+8)*(x2+2x-2)时随意取了一个x的值进行计算,得出结果是-4,小丽告诉小明计算错了,问小丽是如何判断的.
相关试题

