【题目】两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连结DC.
(1)请猜想:DC与BE的数量关系,并给予证明;
(2)求证:DC⊥BE.

参考答案:
【答案】(1)DC=BE;(2)详见解析;
【解析】
(1)根据等腰直角三角形的性质,可以得出△ABE≌△ACD,得出对应边相等即可;
(2)由△ABE≌△ACD可以得出∠B=∠ACD=45°,进而得出∠DCB=90°,就可以得出结论.
(1)解:DC=BE;
理由如下:∵△ABC与△AED均为等腰直角三角形,
∴AB=AC,AE=AD,∠BAC=∠EAD=90°.∠ABC=∠ACB=45°,
∴∠BAC+∠CAE=∠EAD+∠CAE.
即∠BAE=∠CAD,
在△ABE与△ACD中,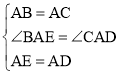 ,
,
∴△ABE≌△ACD(SAS),
∴DC=BE;
(2)证明:∵△ABE≌△ACD,
∴∠ACD=∠ABE=45°,
又∵∠ACB=45°,
∴∠BCD=∠ACB+∠ACD=90°,
∴DC⊥BE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交AD于点F,AE与BF交于点P,连接EF,PD.

(1)求证:四边形ABEF是菱形;
(2)若AB=4,AD=6,∠ABC=60°,求tan∠DPF的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,对角线AC、BD相交于点O,E、F是对角线AC上的两点,当E、F满足下列哪个条件时,四边形DEBF不一定是平行四边形的是( )
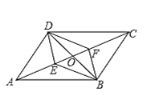
A. AE=CFB. DE=BF
C. ∠ADE=∠CBFD. ∠ABE=∠CDF
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式或不等式组
(1)3(x﹣1)<x﹣(2x﹣1)
(2)

(3)
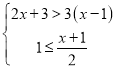
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1)是用硬纸板做成的两个全等的直角三角形,两直角边的长分别为
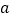 和
和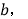 斜边长为
斜边长为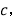 图(2)是以
图(2)是以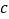 为直角边的等腰直角三角形.请你开动脑筋,将它们拼成一个直角梯形.
为直角边的等腰直角三角形.请你开动脑筋,将它们拼成一个直角梯形.(1)在图(3)处画出拼成的这个图形的示意图;
(2)利用(1)画出的图形证明勾股定理.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,四边形
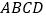 中,
中, ,
, ,
, ,且
,且 ,
,试求:(1)
 的度数;(2)四边形
的度数;(2)四边形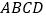 的面积(结果保留根号);
的面积(结果保留根号);
-
科目: 来源: 题型:
查看答案和解析>>【题目】己知:如图,E、F分别是ABCD的AD、BC边上的点,且AE=CF.

(1)求证:△ABE≌△CDF;
(2)若M、N分别是BE、DF的中点,连接MF、EN,试判断四边形MFNE是怎样的四边形,并证明你的结论.
相关试题

