【题目】已知抛物线y=﹣x2+2x+m.
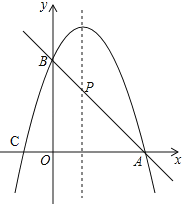
(1)如果抛物线过点A(3,0),与y轴交于点B,求抛物线的解析式及点B、C的坐标;
(2)如图,直线AB与这条抛物线的对称轴交于点P,求直线AB的表达式和点P的坐标.
(3)该抛物线有一点D(x,y),使得S△ABC=S△ACD,求点D的坐标.
参考答案:
【答案】(1)B(0,3);(2)P(1,2);(3)D的坐标为(2,3)或(1﹣![]() ,﹣3)或(1+
,﹣3)或(1+![]() ,﹣3).
,﹣3).
【解析】
试题分析:(1)代入A点的坐标求得m的值即可求得解析式,分别令x=0和y=0,列出方程,解方程即可求得B、C的坐标;
(2)根据待定系数法求得直线AB的解析式,求得抛物线的对称轴x=1,把x=1代入直线的解析式即可求得P的坐标;
(3)根据面积相等且底边相等的三角形的高也应该相等得出D的纵坐标为±3,代入抛物线的解析式即可求得.
解:(1)∵抛物线过点A(3,0),
∴0=﹣9+6+m,
解得m=3,
∴抛物线的解析式为y=﹣x2+2x+3,
令y=0,则,﹣x2+2x+3=0,
解得x1=3,x2=﹣1,
∴C(﹣1,0),
令x=0,得y=3,
∴B(0,3);
(2)∵A(3,0),B(0,3),
设直线AB的解析式为y=kx+b,
∴![]() ,解得
,解得![]() ,
,
∴直线AB的解析式为y=﹣x+3,
∵抛物线y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴对称轴x=1,
把x=1代入y=﹣x+3得y=2,
∴P(1,2);
(3)根据题意得D的纵坐标为±3,
把y=3代入y=﹣x2+2x+3得,﹣x2+2x+3=3,
解得x=0或2,
把y=﹣3代入y=﹣x2+2x+3得,﹣x2+2x+3=﹣3,
解得x=1![]() ,
,
∴D的坐标为(2,3)或(1﹣![]() ,﹣3)或(1+
,﹣3)或(1+![]() ,﹣3).
,﹣3).
-
科目: 来源: 题型:
查看答案和解析>>【题目】按要求解下列方程
(1)x2+2x﹣8=0(用配方法)
(2)x2﹣x﹣3=0(用公式法)
(3)3x(x﹣1)=2(x﹣1)(用因式分解法)
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD是正方形,△ADF旋转一定角度后得到△ABE,如图所示,如果AF=4,AB=7,
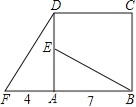
(1)指出旋转中心和旋转角度;
(2)求DE的长度;
(3)BE与DF的位置关系如何?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个3×2的矩形(即长为3,宽为2)可以用两种不同的方式分割成3或6个边长是正整数的小正方形,即:小正方形的个数最多是6个,最少是3个.
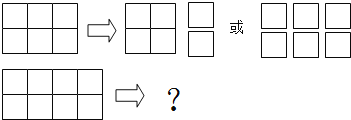
(1)一个5×2的矩形用不同的方式分割后,小正方形的个数最多是 个,最少是 个;
(2)一个7×2的矩形用不同的方式分割后,小正方形的个数最多是 个,最少是 个;
(3)一个(2n+1)×2的矩形用不同的方式分割后,小正方形的个数最多是 个,最少是 个.(n是正整数)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种水果第一天以2元的价格卖出a斤,第二天以1.5元的价格卖出b斤,第三天以1.2元的价格卖出c斤,求:
(1)这三天共卖出水果多少斤?
(2)这三天共卖得多少元?
(3)这三天平均售价是多少?并计算当a=30,b=40,c=50时,平均售价是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点.

(1)求该抛物线的解析式;
(2)用配方法求该抛物线的对称轴以及顶点坐标;
(3)根据图象回答,当x为何值时,y>0,当x为何值时,y<0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】 “囧”(jiǒng)曾经是一个风靡网络的流行词,像一个人脸郁闷的神情.如图所示,一张边长为20的正方形的纸片,剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案(阴影部分).设剪去的小长方形长和宽分别为x、y,剪去的两个小直角三角形的两直角边长也分别为x、y.
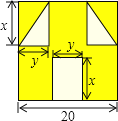
(1)用含有x、y的代数式表示右图中“囧”(阴影部分)的面积;
(2)当x=2y=8时,求此时“囧”的面积;
相关试题

