【题目】按要求解下列方程
(1)x2+2x﹣8=0(用配方法)
(2)x2﹣x﹣3=0(用公式法)
(3)3x(x﹣1)=2(x﹣1)(用因式分解法)
参考答案:
【答案】(1)x1=2,x2=﹣4;(2)x1=![]() ,x2=
,x2=![]() ;(3)x1=
;(3)x1=![]() ,x2=1.
,x2=1.
【解析】
试题分析:(1)先移项,然后进行配方,再开方即可;
(2)首先找出方程中a,b和c的值,求出b2﹣4ac的值,再利用求根公式求出方程的根;
(3)提取公因式(x﹣1)可得(3x﹣2)(x﹣1)=0,再解两个一元一次方程即可.
解:(1)∵x2+2x﹣8=0,
∴x2+2x=8,
∴(x+1)2=9,
∴x+1=±3,
∴x1=2,x2=﹣4;
(2)∵x2﹣x﹣3=0,
∴a=1,b=﹣1,c=﹣3,
∴b2﹣4ac=1+12=13,
∴x=![]() =
=![]() ,
,
∴x1=![]() ,x2=
,x2=![]() ;
;
(3)∵3x(x﹣1)=2(x﹣1),
∴(3x﹣2)(x﹣1)=0,
∴3x﹣2=0或x﹣1=0,
∴x1=![]() ,x2=1.
,x2=1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:
(1)(3a2-ab+7)-(5ab-4a2+7),其中, a=2,b=
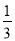 ;
;(2)3(ab-5b2+2a2)-(7ab+16a2-25b2),其中|a-1|+(b+1)2=0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某游乐场在暑假期间推出学生个人门票优惠活动,各类门票价格如下表:

某慈善单位欲购买三种类型的门票共100张奖励品学兼优的留守学生,设购买A种票x张,B种票张数是A种票的3倍还多7张,C种票y张,根据以上信息解答下列问题:
(1)直接写出x与y之间的函数关系式;
(2)设购票总费用为W元,求W(元)与x(张)之间的函数关系式;
(3)为方便学生游玩,计划购买学生的夜场票不低于20张,且节假日通票至少购买5张,有哪几种购票方案?哪种方案费用最少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数的图象经过(2,5)和(﹣1,2)两点.
(1)求此一次函数的解析式;
(2)用描点法在坐标系中画出这个函数的图象,求函数图象与x轴交点A、与y轴交点B的坐标;
(3)求△AOB的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD是正方形,△ADF旋转一定角度后得到△ABE,如图所示,如果AF=4,AB=7,
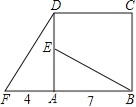
(1)指出旋转中心和旋转角度;
(2)求DE的长度;
(3)BE与DF的位置关系如何?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个3×2的矩形(即长为3,宽为2)可以用两种不同的方式分割成3或6个边长是正整数的小正方形,即:小正方形的个数最多是6个,最少是3个.
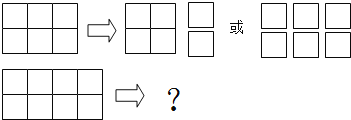
(1)一个5×2的矩形用不同的方式分割后,小正方形的个数最多是 个,最少是 个;
(2)一个7×2的矩形用不同的方式分割后,小正方形的个数最多是 个,最少是 个;
(3)一个(2n+1)×2的矩形用不同的方式分割后,小正方形的个数最多是 个,最少是 个.(n是正整数)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=﹣x2+2x+m.
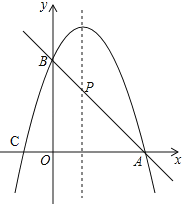
(1)如果抛物线过点A(3,0),与y轴交于点B,求抛物线的解析式及点B、C的坐标;
(2)如图,直线AB与这条抛物线的对称轴交于点P,求直线AB的表达式和点P的坐标.
(3)该抛物线有一点D(x,y),使得S△ABC=S△ACD,求点D的坐标.
相关试题

