【题目】在一次中学生田径运动会上,根据参加男子跳高初赛的运动员的成绩(单位:m),绘制出如下两幅统计图.请根据相关信息,解答下列问题: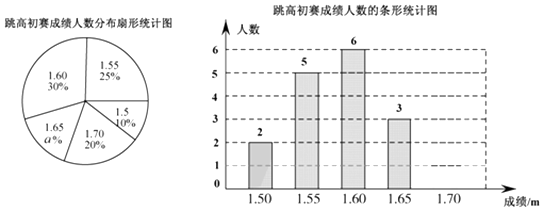
(1)扇形统计图中a= , 初赛成绩为1.70m所在扇形图形的圆心角为°;
(2)补全条形统计图;
(3)这组初赛成绩的众数是 m,中位数是 m;
(4)根据这组初赛成绩确定8人进入复赛,那么初赛成绩为1.60m的运动员杨强能否进入复赛?为什么?
参考答案:
【答案】
(1)15;72
(2)
解:跳170m的人数是: ![]() ×20%=4(人),
×20%=4(人),
补图如下:
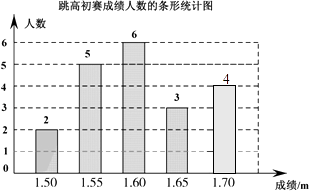
(3)1.60;1.60
(4)
解:不一定,理由如下:因为由高到低的初赛成绩中有4人是1.70m,有3人是1.65m,第8人的成绩为1.60m,但是成绩为1.60m的有6人,所以杨强不一定进入复赛.
【解析】(1.)解:根据题意得:
1﹣20%﹣10%﹣25%﹣30%=15%;
则a的值是15;
初赛成绩为1.70m所在扇形图形的圆心角为:360°×20%=72°;
所以答案是:15,72°;
(3.)解:∵在这组数据中,1.60m出现了6次,出现的次数最多,
∴这组数据的众数是1.60m;
将这组数据从小到大排列,其中处于中间的两个数都是1.60m,
则这组数据的中位数是1.60m.所以答案是:1.60,1.60;
【考点精析】根据题目的已知条件,利用扇形统计图和条形统计图的相关知识可以得到问题的答案,需要掌握能清楚地表示出各部分在总体中所占的百分比.但是不能清楚地表示出每个项目的具体数目以及事物的变化情况;能清楚地表示出每个项目的具体数目,但是不能清楚地表示出各个部分在总体中所占的百分比以及事物的变化情况.
-
科目: 来源: 题型:
查看答案和解析>>【题目】=如图,在半径为2的⊙O中,弦AB=2,⊙O上存在点C,使得弦AC=2
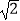 ,则∠BOC=°.
,则∠BOC=°. 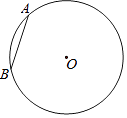
-
科目: 来源: 题型:
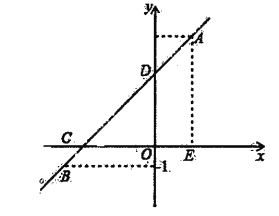
查看答案和解析>>【题目】如图,一次函数的图象l经过点A(2,5),B(-4,-1)两点.
(1)求一次函数表达式.
(2)若点E在x轴上,且E(2,O),点C为直线l与x轴的交点,求△CDE的面积.
(3)你能求出点E到直线l的距离吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读:已知a+b=﹣4,ab=3,求a2+b2的值.
解:∵a+b=﹣4,ab=3,
∴a2+b2=(a+b)2﹣2ab=(﹣4)2﹣2×3=10.
请你根据上述解题思路解答下面问题:
(1)已知a﹣b=﹣3,ab=﹣2,求(a+b)(a2﹣b2)的值.
(2)已知a﹣c﹣b=﹣10,(a﹣b)c=﹣12,求(a﹣b)2+c2的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列各式
(x﹣1)(x+1)=x2﹣1
(x﹣1)(x2+x+1)=x3﹣1
(x﹣1)(x3+x2+x+1)=x4﹣1
(1)根据以上规律,则(x﹣1)(x6+x5+x4+x3+x2+x+1)= ;
(2)你能否由此归纳出一般规律(x﹣1)(xn+xn﹣1+……+x+1)= ;
(3)根据以上规律求32018+32017+32016+…32+3+1的结果.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某月的日历表,在此目历表上可以用一个“十”字圈出5个数.
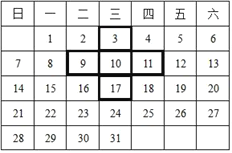
(1)如图中四周的4个数3、9、17、11的和与中间的数10有什么数量关系?
(2)照此方法,任意圈出的5个数是否都具有这样的数量关系?请通过整式的运算说明理由.
(3)用(2)的结论说明圈出的5个数的和能否等于125?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明袋子中有1个红球、1 个绿球和n个白球,这些球除颜色外都相同.
(1)从袋中随机摸出1个球,记录下颜色后放回袋子中并搅匀,不断重复该试验.发现摸到白球的频率稳定在0.75,则n的值为;
(2)当n=2时,把袋中的球搅匀后任意摸出2个球,求摸出的2个球颜色不同的概率.
相关试题

