【题目】如图所示,沿AE折叠矩形,点D恰好落在BC边上的点F处,已知AB=8cm,BC=10cm,求EC的长. 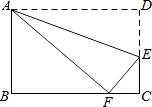
参考答案:
【答案】解:∵四边形ABCD为矩形, ∴AD=BC=10,AB=CD=8,
∵矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上的F处,
∴AF=AD=10,EF=DE,
在Rt△ABF中,∵BF= ![]() =6,
=6,
∴CF=BC﹣BF=10﹣6=4,
设CE=x,则DE=EF=8﹣x
在Rt△ECF中,∵CE2+FC2=EF2 ,
∴x2+42=(8﹣x)2 , 解得x=3,
即CE=3
【解析】先根据矩形的性质得AD=BC=10,AB=CD=8,再根据折叠的性质得AF=AD=10,EF=DE,在Rt△ABF中,利用勾股定理计算出BF=6,则CF=BC﹣BF=4,设CE=x,则DE=EF=8﹣x,然后在Rt△ECF中根据勾股定理得到x2+42=(8﹣x)2 , 再解方程即可得到CE的长.
【考点精析】解答此题的关键在于理解翻折变换(折叠问题)的相关知识,掌握折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】探究规律:如图,已知直线m∥n,A、B为直线n上的两点,C、P为直线m上的两点.
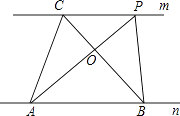
(1)请写出图中面积相等的各对三角形: .
(2)如果A、B、C为三个定点,点P在m上移动,那么无论P点移动到任何位置总有:与△ABC的面积相等;理由是: . -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知抛物线y=x2+bx+c的对称轴为x=2,且其顶点在直线y=﹣2x+2上.
(1)直接写出抛物线的顶点坐标;
(2)求抛物线的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程3x2+2=6x化成一般形式后,二次项系数和一次项系数分别是( )
A. 3、-6B. 3、6C. 3、2D. 2、-6
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两公司为“见义勇为基金会”各捐款60000元,已知乙公司比甲公司人均多捐40元,甲公司的人数比乙公司的人数多20%.
请你根据以上信息,提出一个用分式方程解决的问题,并写出解答过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=13cm,AC=20cm,BC边上的高为12cm,则△ABC的面积为______cm2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点D在△ABC的边AB上,点E为AC的中点,过点C作CF∥AB交DE的延长线于点F,连接AF.

(1)求证:CD=AF;
(2)若∠AED=2∠ECD,求证:四边形ADCF是矩形.
相关试题

