【题目】如图,AE切⊙O于点E,AT交⊙O于点M,N,线段OE交AT于点C,OB⊥AT于点B,已知∠EAT=30°,AE=3 ![]() ,MN=2
,MN=2 ![]() .
. 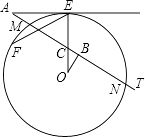
(1)求∠COB的度数;
(2)求⊙O的半径R;
(3)点F在⊙O上( ![]() 是劣弧),且EF=5,把△OBC经过平移、旋转和相似变换后,使它的两个顶点分别与点E,F重合.在EF的同一侧,这样的三角形共有多少个?你能在其中找出另一个顶点在⊙O上的三角形吗?请在图中画出这个三角形,并求出这个三角形与△OBC的周长之比.
是劣弧),且EF=5,把△OBC经过平移、旋转和相似变换后,使它的两个顶点分别与点E,F重合.在EF的同一侧,这样的三角形共有多少个?你能在其中找出另一个顶点在⊙O上的三角形吗?请在图中画出这个三角形,并求出这个三角形与△OBC的周长之比.
参考答案:
【答案】
(1)解:∵AE切⊙O于点E,
∴AE⊥CE,又OB⊥AT,
∴∠AEC=∠CBO=90°,
又∠BCO=∠ACE,
∴△AEC∽△OBC,又∠A=30°,
∴∠COB=∠A=30°
(2)解:∵AE=3 ![]() ,∠A=30°,
,∠A=30°,
∴在Rt△AEC中,tanA=tan30°= ![]() ,即EC=AEtan30°=3,
,即EC=AEtan30°=3,
∵OB⊥MN,∴B为MN的中点,又MN=2 ![]() ,
,
∴MB= ![]() MN=
MN= ![]() ,
,
连接OM,在△MOB中,OM=R,MB= ![]() ,
,
∴OB= ![]() ,
,
在△COB中,∠BOC=30°,
∵cos∠BOC=cos30°= ![]() ,
,
∴BO= ![]() OC,
OC,
∴OC= ![]() OB=
OB= ![]()
![]() ,
,
又OC+EC=OM=R,
∴R= ![]()
![]() +3,
+3,
整理得:R2+18R﹣115=0,即(R+23)(R﹣5)=0,
解得:R=﹣23(舍去)或R=5,
则R=5
(3)解:以EF为斜边,有两种情况,以EF为直角边,有四种情况,所以六种,
画直径FG,连接EG,延长EO与圆交于点D,连接DF,如图所示:
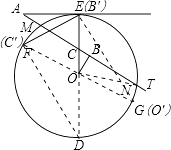
∵EF=5,直径ED=10,可得出∠FDE=30°,
∴FD=5 ![]() ,
,
则C△EFD=5+10+5 ![]() =15+5
=15+5 ![]() ,
,
由(2)可得C△COB=3+ ![]() ,
,
∴C△EFD:C△COB=(15+5 ![]() ):(3+
):(3+ ![]() )=5:1.
)=5:1.
∵EF=5,直径FG=10,可得出∠FGE=30°,
∴EG=5 ![]() ,
,
则C△EFG=5+10+5 ![]() =15+5
=15+5 ![]() ,
,
∴C△EFG:C△COB=(15+5 ![]() ):(3+
):(3+ ![]() )=5:1
)=5:1
【解析】(1)由AE与圆O相切,根据切线的性质得到AE与CE垂直,又OB与AT垂直,可得出两直角相等,再由一对对顶角相等,利用两对对应角相等的两三角形相似可得出三角形AEC与三角形OBC相似,根据相似三角形的对应角相等可得出所求的角与∠A相等,由∠A的度数即可求出所求角的度数;(2)在直角三角形AEC中,由AE及tanA的值,利用锐角三角函数定义求出CE的长,再由OB垂直于MN,由垂径定理得到B为MN的中点,根据MN的长求出MB的长,在直角三角形OBM中,由半径OM=R,及MB的长,利用勾股定理表示出OB的长,在直角三角形OBC中,由表示出OB及cos30°的值,利用锐角三角函数定义表示出OC,用OE﹣OC=EC列出关于R的方程,求出方程的解得到半径R的值;(3)把△OBC经过平移、旋转和相似变换后,使它的两个顶点分别与点E,F重合,在EF的同一侧,这样的三角形共有3个.延长EO与圆交于点D,连接DF,如图所示,由第二问求出半径,的长直径ED的长,根据ED为直径,利用直径所对的圆周角为直角,得到三角形EFD为直角三角形,由∠FDE为30°,利用锐角三角函数定义求出DF的长,表示出三角形EFD的周长,再由第二问求出的三角形OBC的三边表示出三角形BOC的周长,即可求出两三角形的周长之比.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l1∥l2∥l3 , 且l1与l2的距离为1,l2与l3的距离为2,等腰△ABC的顶点分别在直线l1、l2 , l3上,AB=AC,∠BAC=120°,则等腰三角形的腰长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】万安县开发区某电子电路板厂到井冈山大学从应届毕业生中招聘公司职员,对应聘者的专业知识、英语水平、参加社会实践与社团活动等三项进行测试或成果认定,三项的得分满分都为100分,三项的分数分别按5∶3∶2的比例记入每人的最后总分,有4位应聘者的得分如下表所示.
 项目
项目专业知识
英语水平
参加社会实践与
社团活动等
甲
85
85
90
乙
85
85
70
丙
80
90
70
丁
90
90
50
(1)分别算出4位应聘者的总分;
(2)表中四人“专业知识”的平均分为85分,方差为12.5,四人“英语水平”的平均分为87.5分,方差为6.25,请你求出四人“参加社会实践与社团活动等”的平均分及方差;
(3)分析(1)和(2)中的有关数据,你对大学生应聘者有何建议?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知正方形ABCD,直角三角形纸板的一个锐角顶点与点A重合,纸板绕点A旋转时,直角三角形纸板的一边与直线CD交于E,分别过B、D作直线AE的垂线,垂足分别为F、G.
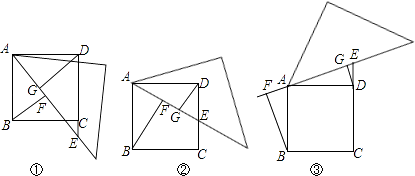
(1)当点E在DC延长线时,如图①,求证:BF=DG﹣FG;
(2)将图①中的三角板绕点A逆时针旋转得图②、图③,此时BF、FG、DG之间又有怎样的数量关系?请直接写出结论(不必证明) -
科目: 来源: 题型:
查看答案和解析>>【题目】某面粉加工厂加工的面粉,用每袋可装10g面粉的袋子装了200袋经过称重,质量超过标准质量10kg的用正数表示,质量低于标准质量10kg的用负数表示,结果记录如下
与标准质量的偏差(kg)
﹣1.5
﹣1
﹣0.5
0
0.5
1
2
袋数(袋)
40
30
10
25
40
20
35
(1)求这批面粉的总质量;
(2)如果100kg小麦加工80kg面粉,那么这批面粉是由多少千克小麦加工的?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了减轻学生课业负担,提高课堂效果,我县教体局积极推进 “高效课堂”建设.
某学校的《课堂检测》印刷任务原来由甲复印店承接,其每月收费y(元)与复印页数x(页)的函数关系如图所示:
⑴从图象中可看出:每月复印超过500页部分每页收费 元;
⑵现在乙复印店表示:若学校先按每月付给200元的月承包费,则可按每页0.15元收费.乙复印店每月收费y(元)与复印页数x(页)的函数关系为 ;
⑶在给出的坐标系内画出(2)中的函数图象,并结合函数图象回答每月复印在3000页左右应选择哪个复印店?

-
科目: 来源: 题型:
查看答案和解析>>【题目】平面内的两条直线有相交和平行两种位置关系.
(1)如图1,若AB∥CD,点P在AB、CD内部,∠B=50°,∠D=30°,求∠BPD.
(2)如图2,将点P移到AB、CD外部,则∠BPD、∠B、∠D之间有何数量关系?(不需证明)
(3)如图3,写出∠BPD﹑∠B﹑∠D﹑∠BQD之间的数量关系?请证明你的结论.
(4)如图4,求出∠A+∠B+∠C+∠D+∠E+∠F的度数.


相关试题

