【题目】如图,直线l1∥l2∥l3 , 且l1与l2的距离为1,l2与l3的距离为2,等腰△ABC的顶点分别在直线l1、l2 , l3上,AB=AC,∠BAC=120°,则等腰三角形的腰长为 . 
参考答案:
【答案】2或 ![]() 或
或 ![]()
【解析】解:①如图1中,作BF⊥l1于F交l3于H,取BC的中点E,过点E作l4∥l3 , 连接AE.取AB的中点O,连接OF、OE. 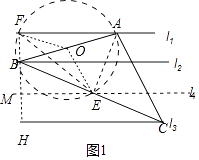
∵AB=AC,BE=EC.
∴AE⊥BC,∠BAE=60°,∵BF⊥AF,
∴∠AFB=∠AEB=90°,
∴OA=OB=OF=OE,
∴A、F、B、E四点共圆,
∴∠BFE=∠BAE=60°,
∵l1∥l2∥l3∥l4 , BE=EC,
∴BF=BM=MH=1,
在Rt△EFM中,EM=FMtan60°=2 ![]() ,
,
在Rt△BEM中,BE= ![]() =
= ![]() ,
,
在Rt△ABE中,AB=BE÷cos30°= ![]() .
.
②如图2中,作BF⊥l3于F交l2于G,取BC的中点E,过点E作 ![]() ∥l1交BF于H.
∥l1交BF于H.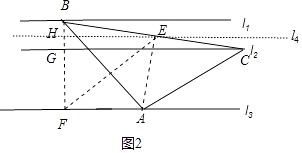
同理可证B、F、A、E四点共圆,
∴∠BFE=∠BAE=60°,
∵BE=EC,l1∥l4∥l2 ,
∴BH=HG= ![]() ,
,
在Rt△EHF中,HE=FHtan60°= ![]() ,
,
在Rt△BEH中,BE= ![]() =
= ![]() ,
,
∴AB=BE÷cos30°= ![]() ,
,
③如图3中,在直线l2取一点A,作AB⊥l2交l3于B,作∠CAB=120°,作CE⊥l2于E.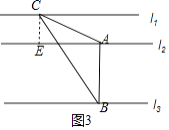
∵∠CAE=∠CAB﹣∠EAB=120°﹣90°=30°,
∴在Rt△ACE中,AC=2EC=2,
∵AB=2,
∴AC=AB,
∴△ABC满足条件,
∴AB=2,
综上所述,等腰三角形的腰长为2或 ![]() 或
或 ![]() .
.
【考点精析】通过灵活运用含30度角的直角三角形,掌握在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(感知)如图①,AB∥CD,点E在直线AB与CD之间,连结AE、BE,试说明∠BEE+∠DCE=∠AEC.下面给出了这道题的解题过程,请完成下面的解题过程,并填空(理由或数学式):
解:如图①,过点E作EF∥AB
∴∠BAE=∠1( )
∵AB∥CD( )
∴CD∥EF( )
∴∠2=∠DCE
∴∠BAE+∠DCE=∠1+∠2( )
∴∠BAE+∠DCE=∠AEC
(探究)当点E在如图②的位置时,其他条件不变,试说明∠AEC+∠FGC+∠DCE=360°;
(应用)点E、F、G在直线AB与CD之间,连结AE、EF、FG和CG,其他条件不变,如图③.若∠EFG=36°,则∠BAE+∠AEF+∠FGC+∠DCG= °.
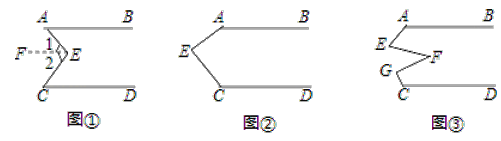
-
科目: 来源: 题型:
查看答案和解析>>【题目】制了下列两幅不完整的统计图,请你根据统计图提供的信息解答以下问题:
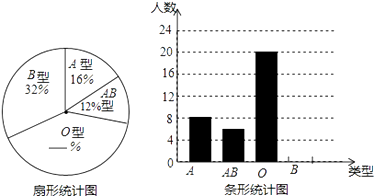
(1)该校七年级(1)班有多少名学生.
(2)求出扇形统计图中“O型”血所对扇形的圆心角的度数.
(3)将条形统计图中“B型”血部分的条形图补充完整. -
科目: 来源: 题型:
查看答案和解析>>【题目】小明投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数:y=﹣10x+500,在销售过程中销售单价不低于成本价,而每件的利润不高于成本价的60%.
(1)设小明每月获得利润为w(元),求每月获得利润w(元)与销售单价x(元)之间的函数关系式,并确定自变量x的取值范围.
(2)当销售单价定为多少元时,每月可获得最大利润?每月的最大利润是多少?
(3)如果小明想要每月获得的利润不低于2000元,那么小明每月的成本最少需要多少元?(成本=进价×销售量) -
科目: 来源: 题型:
查看答案和解析>>【题目】万安县开发区某电子电路板厂到井冈山大学从应届毕业生中招聘公司职员,对应聘者的专业知识、英语水平、参加社会实践与社团活动等三项进行测试或成果认定,三项的得分满分都为100分,三项的分数分别按5∶3∶2的比例记入每人的最后总分,有4位应聘者的得分如下表所示.
 项目
项目专业知识
英语水平
参加社会实践与
社团活动等
甲
85
85
90
乙
85
85
70
丙
80
90
70
丁
90
90
50
(1)分别算出4位应聘者的总分;
(2)表中四人“专业知识”的平均分为85分,方差为12.5,四人“英语水平”的平均分为87.5分,方差为6.25,请你求出四人“参加社会实践与社团活动等”的平均分及方差;
(3)分析(1)和(2)中的有关数据,你对大学生应聘者有何建议?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知正方形ABCD,直角三角形纸板的一个锐角顶点与点A重合,纸板绕点A旋转时,直角三角形纸板的一边与直线CD交于E,分别过B、D作直线AE的垂线,垂足分别为F、G.
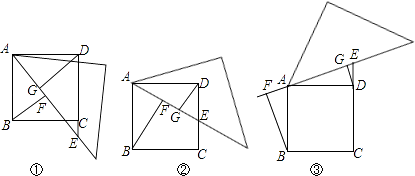
(1)当点E在DC延长线时,如图①,求证:BF=DG﹣FG;
(2)将图①中的三角板绕点A逆时针旋转得图②、图③,此时BF、FG、DG之间又有怎样的数量关系?请直接写出结论(不必证明) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AE切⊙O于点E,AT交⊙O于点M,N,线段OE交AT于点C,OB⊥AT于点B,已知∠EAT=30°,AE=3
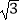 ,MN=2
,MN=2 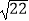 .
. 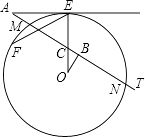
(1)求∠COB的度数;
(2)求⊙O的半径R;
(3)点F在⊙O上(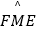 是劣弧),且EF=5,把△OBC经过平移、旋转和相似变换后,使它的两个顶点分别与点E,F重合.在EF的同一侧,这样的三角形共有多少个?你能在其中找出另一个顶点在⊙O上的三角形吗?请在图中画出这个三角形,并求出这个三角形与△OBC的周长之比.
是劣弧),且EF=5,把△OBC经过平移、旋转和相似变换后,使它的两个顶点分别与点E,F重合.在EF的同一侧,这样的三角形共有多少个?你能在其中找出另一个顶点在⊙O上的三角形吗?请在图中画出这个三角形,并求出这个三角形与△OBC的周长之比.
相关试题

