【题目】已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.
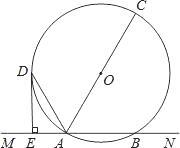
(1)求证:DE是⊙O的切线;
(2)若DE=6cm,AE=3cm,求⊙O的半径.
参考答案:
【答案】解:(1)证明:连接OD,
∵OA=OD,∴∠OAD=∠ODA。
∵∠OAD=∠DAE,∴∠ODA=∠DAE。∴DO∥MN。
∵DE⊥MN,∴∠ODE=∠DEM =90°,即OD⊥DE。
∵D在⊙O上,∴DE是⊙O的切线。
(2)连接CD,

∵∠AED=90°,DE=6,AE=3,∴AD=![]() 。
。
∵AC是⊙O的直径,∴∠ADC=∠AED =90°。
∵∠CAD=∠DAE,∴△ACD∽△ADE。 ∴![]() ,即
,即![]() 。
。
解得:AC=15。
∴⊙O的半径是7.5cm。
【解析】试题分析:(1)连接OD,根据平行线的判断方法与性质可得∠ODE=∠DEM=90°,且D在⊙O上,故DE是⊙O的切线.
(2)由直角三角形的特殊性质,可得AD的长,又有△ACD∽△ADE.根据相似三角形的性质列出比例式,代入数据即可求得圆的半径.
试题解析:(1)证明:连接OD.
∵OA=OD,
∴∠OAD=∠ODA.
∵∠OAD=∠DAE,
∴∠ODA=∠DAE.
∴DO∥MN.
∵DE⊥MN,
∴∠ODE=∠DEM=90°.
即OD⊥DE.
∵D在⊙O上,OD为⊙O的半径,
∴DE是⊙O的切线.
(2)解:∵∠AED=90°,DE=6,AE=3,
∴![]() .
.
连接CD.
∵AC是⊙O的直径,
∴∠ADC=∠AED=90°.
∵∠CAD=∠DAE,
∴△ACD∽△ADE.
∴![]() .
.
∴![]() .
.
则AC=15(cm).
∴⊙O的半径是7.5cm.

-
科目: 来源: 题型:
查看答案和解析>>【题目】解决下面问题:
如图,在△ABC中,∠A是锐角,点D,E分别在AB,AC上,且
 ,BE与CD相交于点O,探究BD与CE之间的数量关系,并证明你的结论.
,BE与CD相交于点O,探究BD与CE之间的数量关系,并证明你的结论.
小新同学是这样思考的:
在平时的学习中,有这样的经验:假如△ABC是等腰三角形,那么在给定一组对应条件,如图a,BE,CD分别是两底角的平分线(或者如图b,BE,CD分别是两条腰的高线,或者如图c,BE,CD分别是两条腰的中线)时,依据图形的轴对称性,利用全等三角形和等腰三角形的有关知识就可证得更多相等的线段或相等的角.这个问题也许可以通过添加辅助线构造轴对称图形来解决.

图a 图b 图c
请参考小新同学的思路,解决上面这个问题..
-
科目: 来源: 题型:
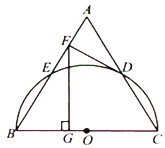
查看答案和解析>>【题目】如图,以等边三角形ABC的BC边为直径画半圆,分别交AB、AC于点E、D,DF是圆的切线,过点F作BC的垂线交BC于点G.若AF的长为2,则FG的长为
A. 4 B.
 C. 6 D.
C. 6 D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】衢州新闻网2月16日讯,2013年春节“黄金周”全市接待游客总数为833100人次.将数833100用科学记数法表示应为( )
A.0.833×106
B.83.31×105
C.8.331×105
D.8.331×104 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC的平分线BF与△ABC的外角平分线CF相交于点F,过F作DF∥BC,交AB于D,交AC于E。
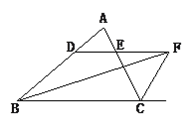
(1)写出图中所有的等腰三角形,并选择其中一个说明理由。
(2)直接写出BD,CE,DE之间的数量关系。
(3)若DE=5cm,CE=8cm,BF=24cm,求△BDF的面积。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果出售一个商品,获利记为正,则-20元表示。
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个角的补角是它的余角的4倍,则这个角是_________度.
相关试题

