搜索
【题目】如图，在矩形ABCD中，AD=2AB，点M、N分别在边AD、BC上，连接BM、DN．若四边形MBND是菱形，则 
等于（ ）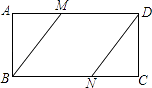 
A.
B.
C.
D.
参考答案：
【答案】C
【解析】解：∵四边形MBND是菱形，
∴MD=MB．
∵四边形ABCD是矩形，
∴∠A=90°．
设AB=x，AM=y，则MB=2x﹣y，（x、y均为正数）．
在Rt△ABM中，AB2+AM2=BM2 ， 即x2+y2=（2x﹣y）2 ，
解得x= 
y，
∴MD=MB=2x﹣y= 
y，
∴ 
= 
= 
．
故选：C．
【考点精析】掌握勾股定理的概念和菱形的性质是解答本题的根本，需要知道直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；菱形的四条边都相等；菱形的对角线互相垂直，并且每一条对角线平分一组对角；菱形被两条对角线分成四个全等的直角三角形；菱形的面积等于两条对角线长的积的一半．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，已知A（-3，0），B（0，
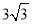），点D与点A关于y轴对称，C在第一象限内且四边形ABCD是平行四边形.（1）求点C、点D的坐标并用尺规作图确定两点位置（保留作图痕迹）
（2）若半径为1的⊙P从点A出发，沿A—D—B—C以每秒4个单位长的速度匀速移动，同时⊙P的半径以每秒0.5个单位长的速度增加，运动到点C时运动停止，当运动时间为t秒时
①t为何值时，⊙P与y轴相切？
②在整个运动过程中⊙P与y轴有公共点的时间共有几秒？简述过程.
（3）若线段AB绕点O顺时针旋转90°，线段AB扫过的面积是多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，EF∥AD，∠1=∠2，∠B=35°，将求∠BDG的过程填写完整． 解：∵EF∥AD，
∴∠2=（）
又∵∠1=∠2
∴∠1=（ 等量代换 ）
∴DG∥（）
∴∠B+=180°（）
∵∠B=35°
∴∠BDG= ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】今年我市某公司分两次采购了一批大蒜，第一次花费40万元，第二次花费60万元．已知第一次采购时每吨大蒜的价格比去年的平均价格上涨了500元，第二次采购时每吨大蒜的价格比去年的平均价格下降了500元，第二次的采购数量是第一次采购数量的两倍．
（1）试问去年每吨大蒜的平均价格是多少元？
（2）该公司可将大蒜加工成蒜粉或蒜片，若单独加工成蒜粉，每天可加工8吨大蒜，每吨大蒜获利1000元；若单独加工成蒜片，每天可加工12吨大蒜，每吨大蒜获利600元．由于出口需要，所有采购的大蒜必需在30天内加工完毕，且加工蒜粉的大蒜数量不少于加工蒜片的大蒜数量的一半，为获得最大利润，应将多少吨大蒜加工成蒜粉？最大利润为多少？ -
科目： 来源： 题型：
查看答案和解析>>【题目】2的相反数是 ．
-
科目： 来源： 题型：
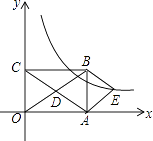
查看答案和解析>>【题目】如图，在平面直角坐标系中．矩形OABC的对角线OB，AC相交于点D，且BE∥AC，AE∥OB．如果OA=3，OC=2，则经过点E的反比例函数解析式为（ ）
A.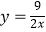
B.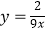
C.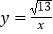
D.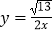
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在□ABCD中，点E、F分别是AD、BC的中点，分别连接BE、DF、BD．
（1）求证：△AEB≌△CFD；
（2）若四边形EBFD是菱形，求∠ABD的度数．
相关试题
