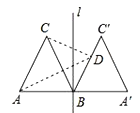
【题目】如图,等边三角形ABC的边长为2,过点B的直线![]() ⊥AB,且△ABC与△A′BC′关于直线
⊥AB,且△ABC与△A′BC′关于直线![]() 对称,D为线段BC′上一动点,则AD + CD的最小值是( )
对称,D为线段BC′上一动点,则AD + CD的最小值是( )
A. 4 B. ![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】A
【解析】连接CC′,连接A′C交y轴于点D,连接AD,此时AD+CD的值最小,根据等边三角形的性质即可得出四边形CBA′C′为菱形,根据菱形的性质即可求出A′C的长度,从而得出结论.
解:连接CC′,连接A′C交l于点D,连接AD,此时AD+CD的值最小,如图所示.
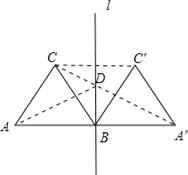

∵△ABC与△A′BC′为正三角形,
∴∠ABC=∠A/=60°,A/B/=BC=A/C/,
∴A/C/∥BC,
∴四边形A/BCC/为菱形,
∴点C关于BC/对称的点是A/,
∴当点D与点B重合时,AD+CD取最小值,
此时AD+CD=2+2=4.
故选A.
“点睛”本题考查了轴对称中的最短线路问题以及等边三角形的性质,找出点C关于BC/对称的点是A/是解题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两名运动员,在相同情况下各射击10次,两名的平均数都是8,方差分别为4和2.2,则成绩较好的是__________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的方程x2﹣mx+n=0没有实数解,则抛物线y=x2﹣mx+n与x轴的交点有( )
A.2个B.1个C.0个D.不能确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CE=2DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③EG=DE+BG;④AG∥CF;⑤S△FGC=3.6.其中正确结论的个数是( )
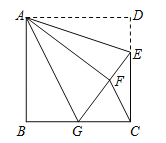
A.2 B.3 C.4 D.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个多项式与2x2﹣3x﹣1的和等于x2﹣2x﹣3,则这个多项式是( )
A.﹣x2+2x+2
B.﹣x2+x+2
C.x2﹣x+2
D.﹣x2+x﹣2 -
科目: 来源: 题型:
查看答案和解析>>【题目】星期天,玲玲骑自行车到郊外游玩,她离家的距离与时间的关系如图所示,请根据图象回答下列问题.
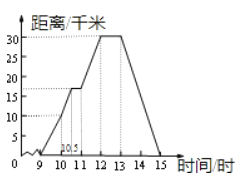
(1)玲玲到达离家最远的地方是什么时间?离家多远?
(2)她何时开始第一次休息?休息了多长时间?
(3)她骑车速度最快是在什么时候?车速多少?
(4)玲玲全程骑车的平均速度是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】(3x2y﹣2x+1)(﹣2xy)
相关试题

