【题目】等腰Rt△ABC中,∠BAC=90°,AB=AC,点A、点B分别是y轴、x轴上两个动点,直角边AC交x轴于点D,斜边BC交y轴于点E;
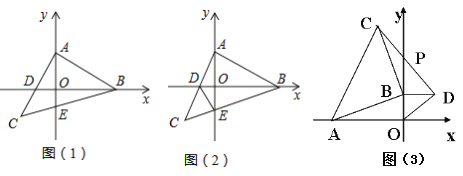
(1)如图(1),已知C点的横坐标为-1,直接写出点A的坐标;
(2)如图(2), 当等腰Rt△ABC运动到使点D恰为AC中点时,连接DE,求证:∠ADB=∠CDE;
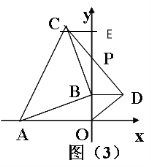
(3)如图(3), 若点A在x轴上,且A(-4,0),点B在y轴的正半轴上运动时,分别以OB、AB为直角边在第一、二象限作等腰直角△BOD和等腰直角△ABC,连结CD交y轴于点P,问当点B在y轴的正半轴上运动时,BP的长度是否变化?若变化请说明理由,若不变化,请求出BP的长度.
参考答案:
【答案】(1)A(0,1);(2)证明见解析;(3)BP的长度不变;理由见解析.
【解析】
试题分析:(1)过点C作![]() 轴于点F,易证
轴于点F,易证![]() ,∴CF=OA=1,∴A(0,1);
,∴CF=OA=1,∴A(0,1);
(2)过点C作![]() 交y轴于点G,易证
交y轴于点G,易证![]() ,则可得CG=AD=CD,由于∠ADB=∠CGA,
,则可得CG=AD=CD,由于∠ADB=∠CGA,
∠DCE=∠GCE=45°,可证![]() ,则∠CDE=∠AGC,∴∠ADB=∠CDE;
,则∠CDE=∠AGC,∴∠ADB=∠CDE;
![]()
![]() (3)过点C作CE⊥y轴于点E,∵∠BAC=90°,∴∠CBE+∠ABO=90°,可证△CBE≌△BAO,∴CE=BO,BE=AO=4,∵BD=BO,∴CE=BD.可证△CPE≌△DPB.∴BP=EP=2 .
(3)过点C作CE⊥y轴于点E,∵∠BAC=90°,∴∠CBE+∠ABO=90°,可证△CBE≌△BAO,∴CE=BO,BE=AO=4,∵BD=BO,∴CE=BD.可证△CPE≌△DPB.∴BP=EP=2 .
试题解析:
(1)如图,过点C作![]() 轴于点F,易证
轴于点F,易证![]() (AAS),
(AAS),
∴CF=OA=1,
∴A(0,1);
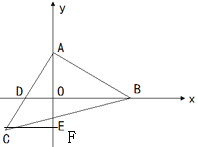
(2)如图,过点C作![]() 交y轴于点G,则
交y轴于点G,则![]() (ASA),
(ASA),
∴CG=AD=CD,∠ADB=∠CGA,
∵∠DCE=∠GCE=45°,
∴![]() (SAS),
(SAS),
∴∠CDE=∠AGC,
∴∠ADB=∠CDE;
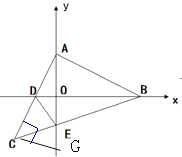
(4)BP的长度不变,理由如下:
过点C作CE⊥y轴于点E,
∵∠BAC=90°,
∴∠CBE+∠ABO=90°,
∵∠BAO+∠ABO=90°,
∴∠CBE=∠BAO.
∵∠CEB=∠AOB=90°,AB=AC,
∴△CBE≌△BAO(AAS),
![]() ∴CE=BO,BE=AO=4,
∴CE=BO,BE=AO=4,
∵BD=BO,∴CE=BD.
∵∠CEP=∠DBP=90°, ∠CPE=∠DPB,
∴△CPE≌△DPB(AAS).
![]() ∴BP=EP=2 .
∴BP=EP=2 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】电子跳蚤游戏盘是如图所示的△ABC,AB=8,AC=9,BC=10,如果跳蚤开始时在BC边的点P0处, BP0=4.跳蚤第一步从P0跳到AC边的P1(第1次落点)处,且CP1=CP0;第二步从P1跳到AB边的P2(第2次落点)处,且AP2=AP1;第三步从P2跳到BC边的P3(第3次落点)处,且BP3=BP2;跳蚤按上述规则一直跳下去,第n次落点为Pn(n为正整数),则点P2015与A间的距离为( )

A.3 B.4 C.5 D.6
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列一组图形中点的个数,其中第1个图中共有4个点,第2个图中共有10个点,第3个图中共有19个点,…按此规律第7个图中共有点的个数是( )

A.46 B.85 C.72 D.66
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线经过三点A(1,0),B(4,0),C(0,﹣2).
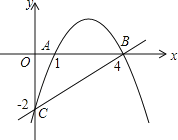
(1)求出抛物线的解析式;
(2)P是抛物线上一动点,过P作PM⊥x轴,垂足为M,是否存在P点,使得以B,P,M为顶点的三角形与△OBC相似(相似比不为1)?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】

(1)移动1次后该点到原点的距离为 个单位长度;
(2)移动2次后该点,到原点的距离为 个单位长度;
(3)移动3次后该点到原点的距离为 个单位长度;
(4)试问移动n次后该点到原点的距离为多少个单位长度?
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)﹣3+5.3+7﹣5.3
(2)0.35+(﹣0.6)+0.25+(﹣5.4)
(3)

(4)
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形AOCB在平面直角坐标系xoy中,点O为原点,点B在反比例函数
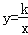 (x>0)图象上,△BOC的面积为8.
(x>0)图象上,△BOC的面积为8.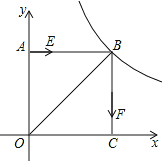
(1)求反比例函数
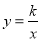 的关系
的关系(2)若动点E从A开始沿AB向B以每秒1个单位的速度运动,同时动点F从B开始沿BC向C以每秒2个单位的速度运动,当其中一个动点到达端点时,另一个动点随之停止运动.若运动时间用t表示,△BEF的面积用S表示,求出S关于t的函数关系式?
(3)当运动时间为
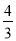 秒时,在坐标轴上是否存在点P,使△PEF的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由.
秒时,在坐标轴上是否存在点P,使△PEF的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由.
相关试题

