【题目】如图,抛物线经过三点A(1,0),B(4,0),C(0,﹣2).
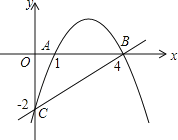
(1)求出抛物线的解析式;
(2)P是抛物线上一动点,过P作PM⊥x轴,垂足为M,是否存在P点,使得以B,P,M为顶点的三角形与△OBC相似(相似比不为1)?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)此抛物线的解析式为![]() .(2)存在.符合条件的点P为(2,1)或(5,﹣2)或(﹣3,﹣14).
.(2)存在.符合条件的点P为(2,1)或(5,﹣2)或(﹣3,﹣14).
【解析】
试题分析:(1)本题需先根据已知条件,过C点,设出该抛物线的解析式为y=ax2+bx﹣2,再根据过A,B两点,即可得出结果.
(2)本题首先判断出存在,首先设出横坐标和纵坐标,从而得出PA的解析式,再分三种情况进行讨论,当![]() =
=![]() 时和
时和![]() 时,当P,C重合时,△APM≌△ACO,分别求出点P的坐标即可.
时,当P,C重合时,△APM≌△ACO,分别求出点P的坐标即可.
解:(1)∵该抛物线过点C(0,﹣2),
∴可设该抛物线的解析式为y=ax2+bx﹣2.
将A(1,0),B(4,0)代入,
得![]() ,解得
,解得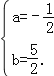 ,
,
∴此抛物线的解析式为![]() .
.
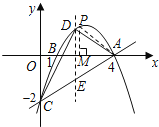
(2)存在.如图,设P点的横坐标为m,
则P点的纵坐标为﹣![]() m2+
m2+![]() m﹣2,
m﹣2,
当1<m<4时,AM=4﹣m,PM=﹣﹣![]() m2+
m2+![]() m﹣2,
m﹣2,
又∵∠COA=∠PMA=90°,
∴①当![]() =
=![]() 时,
时,
∵C在抛物线上,
∴OC=2,
∵OA=4,
∴![]() =
=![]() =2时,
=2时,
∴△APM∽△ACO,
即4﹣m=2(﹣![]() m2+
m2+![]() m﹣2),
m﹣2),
解得m1=2,m2=4(舍去),
∴P(2,1).
②当![]() 时,△APM∽△CAO,即2(4﹣m)=﹣
时,△APM∽△CAO,即2(4﹣m)=﹣![]() m2+
m2+![]() m﹣2,
m﹣2,
解得m1=4,m2=5(均不合题意,舍去)
∴当1<m<4时,P(2,1),
当m>4时,AM=m﹣4,PM=![]() m2﹣
m2﹣![]() m+2,
m+2,
①![]() ,②
,②![]() =
=![]() 时,
时,
把P(m,﹣![]() m2+
m2+![]() m﹣2),代入得:2(﹣
m﹣2),代入得:2(﹣![]() m2+
m2+![]() m﹣2)=m﹣4,2(m﹣4)=﹣
m﹣2)=m﹣4,2(m﹣4)=﹣![]() m2+
m2+![]() m﹣2,
m﹣2,
解得:第一个方程的解是m=﹣2﹣2![]() <4(舍去)m=﹣2+2
<4(舍去)m=﹣2+2![]() <4(舍去),
<4(舍去),
第二个方程的解是m=5,m=4(舍去)
求出m=5,=﹣![]() m2+
m2+![]() m﹣2=﹣2,
m﹣2=﹣2,
则P(5,﹣2),
当m<1时,AM=4﹣m,PM=﹣![]() m2+
m2+![]() m﹣2,
m﹣2,
①![]() ,②
,②![]() =
=![]() 时,
时,
则:2(![]() m2﹣
m2﹣![]() m+2)=4﹣m,2(4﹣m)=
m+2)=4﹣m,2(4﹣m)=![]() m2﹣
m2﹣![]() m+2,
m+2,
解得:第一个方程的解是m=0(舍去),m=4(舍去),第二个方程的解是m=4(舍去),m=﹣3,
m=﹣3时,﹣![]() m2+
m2+![]() m﹣2=﹣14,
m﹣2=﹣14,
则P(﹣3,﹣14),
综上所述,符合条件的点P为(2,1)或(5,﹣2)或(﹣3,﹣14),
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们可以用几何图形来解决一些代数问题,如图(甲)可以来解释(a+b)2=a2+2ab+b2,
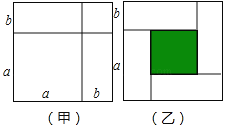
(1)图(乙)是四张全等的矩形纸片拼成的图形,请利用图中阴影部分面积的不同表示方法,写出一个关于a,b代数恒等式表示 ;
(2)请构图解释:(a+b+c)2=a2+b2+c2+2ab+2bc+2ac;
(3)请通过构图因式分解:a2+3ab+2b2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】电子跳蚤游戏盘是如图所示的△ABC,AB=8,AC=9,BC=10,如果跳蚤开始时在BC边的点P0处, BP0=4.跳蚤第一步从P0跳到AC边的P1(第1次落点)处,且CP1=CP0;第二步从P1跳到AB边的P2(第2次落点)处,且AP2=AP1;第三步从P2跳到BC边的P3(第3次落点)处,且BP3=BP2;跳蚤按上述规则一直跳下去,第n次落点为Pn(n为正整数),则点P2015与A间的距离为( )

A.3 B.4 C.5 D.6
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列一组图形中点的个数,其中第1个图中共有4个点,第2个图中共有10个点,第3个图中共有19个点,…按此规律第7个图中共有点的个数是( )

A.46 B.85 C.72 D.66
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰Rt△ABC中,∠BAC=90°,AB=AC,点A、点B分别是y轴、x轴上两个动点,直角边AC交x轴于点D,斜边BC交y轴于点E;
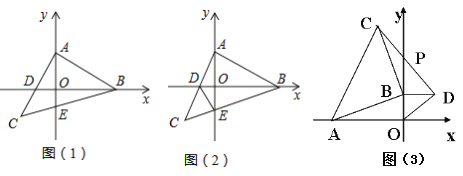
(1)如图(1),已知C点的横坐标为-1,直接写出点A的坐标;
(2)如图(2), 当等腰Rt△ABC运动到使点D恰为AC中点时,连接DE,求证:∠ADB=∠CDE;
(3)如图(3), 若点A在x轴上,且A(-4,0),点B在y轴的正半轴上运动时,分别以OB、AB为直角边在第一、二象限作等腰直角△BOD和等腰直角△ABC,连结CD交y轴于点P,问当点B在y轴的正半轴上运动时,BP的长度是否变化?若变化请说明理由,若不变化,请求出BP的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】

(1)移动1次后该点到原点的距离为 个单位长度;
(2)移动2次后该点,到原点的距离为 个单位长度;
(3)移动3次后该点到原点的距离为 个单位长度;
(4)试问移动n次后该点到原点的距离为多少个单位长度?
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)﹣3+5.3+7﹣5.3
(2)0.35+(﹣0.6)+0.25+(﹣5.4)
(3)

(4)
 .
.
相关试题

