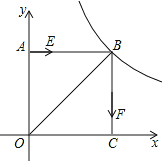
【题目】如图,正方形AOCB在平面直角坐标系xoy中,点O为原点,点B在反比例函数![]() (x>0)图象上,△BOC的面积为8.
(x>0)图象上,△BOC的面积为8.
(1)求反比例函数![]() 的关系
的关系
(2)若动点E从A开始沿AB向B以每秒1个单位的速度运动,同时动点F从B开始沿BC向C以每秒2个单位的速度运动,当其中一个动点到达端点时,另一个动点随之停止运动.若运动时间用t表示,△BEF的面积用S表示,求出S关于t的函数关系式?
(3)当运动时间为![]() 秒时,在坐标轴上是否存在点P,使△PEF的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由.
秒时,在坐标轴上是否存在点P,使△PEF的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)、y=![]() ;(2)、S=-
;(2)、S=-![]() +4;(3)、P(
+4;(3)、P(![]() ,0)
,0)
【解析】
试题分析:(1)、设点B的坐标为(a,a),根据三角形的面积得出a的值,然后求出点B的坐标,计算反比例函数的解析式;(2)、根据题意得出AE=t,BF=2t,BE=4-t,然后求出函数解析式;(3)、首先根据t的值求出点E和点F的坐标,作F点关于x轴的对称点![]() ,求出直线E
,求出直线E![]() 的直线解析式,从而得出点P的坐标.
的直线解析式,从而得出点P的坐标.
试题解析:(1)、∵四边形AOCB为正方形,
∴AB=BC=OC=OA,
设点B坐标为(a,a),
∵![]() C=8,
C=8,
∴![]() =8,
=8,
∴a=±4
又∵点B在第一象限,
∴点B坐标为(4,4),
将点B(4,4)代入y=![]() 得,k=16
得,k=16
∴反比例函数解析式为y=![]()
(2)、∵运动时间为t,
∴AE=t,BF=2t
∵AB=4,
∴BE=4-t,
∴![]() =
=![]() (4-t)2t=-
(4-t)2t=-![]() +4t=--
+4t=--![]() +4,
+4,
(3)、存在.
当t=![]() 时,点E的坐标为(
时,点E的坐标为(![]() ,4),点F的坐标为(4,
,4),点F的坐标为(4,![]() )
)
作F点关于x轴的对称点![]() ,得F1(4,-
,得F1(4,-![]() ),经过点E、
),经过点E、![]() 作直线
作直线
由E(![]() ,4),
,4),![]() (4,-
(4,-![]() )代入y=ax+b得:
)代入y=ax+b得:
解得:
可得直线E![]() 的解析式是y=-2x+
的解析式是y=-2x+![]()
当y=0时,x=![]()
∴P点的坐标为(![]() ,0)
,0)

-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰Rt△ABC中,∠BAC=90°,AB=AC,点A、点B分别是y轴、x轴上两个动点,直角边AC交x轴于点D,斜边BC交y轴于点E;
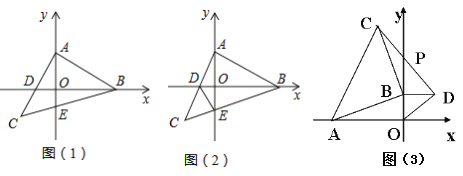
(1)如图(1),已知C点的横坐标为-1,直接写出点A的坐标;
(2)如图(2), 当等腰Rt△ABC运动到使点D恰为AC中点时,连接DE,求证:∠ADB=∠CDE;
(3)如图(3), 若点A在x轴上,且A(-4,0),点B在y轴的正半轴上运动时,分别以OB、AB为直角边在第一、二象限作等腰直角△BOD和等腰直角△ABC,连结CD交y轴于点P,问当点B在y轴的正半轴上运动时,BP的长度是否变化?若变化请说明理由,若不变化,请求出BP的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】

(1)移动1次后该点到原点的距离为 个单位长度;
(2)移动2次后该点,到原点的距离为 个单位长度;
(3)移动3次后该点到原点的距离为 个单位长度;
(4)试问移动n次后该点到原点的距离为多少个单位长度?
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)﹣3+5.3+7﹣5.3
(2)0.35+(﹣0.6)+0.25+(﹣5.4)
(3)

(4)
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组数中,是勾股数的是( )
A. 1,2,3 B. 2,3,4 C. 1.5 ,2,2.5 D. 6,8,10
-
科目: 来源: 题型:
查看答案和解析>>【题目】某农舍大门是一个木制矩形栏栅,它高为2m,宽为1.5m,现需要在相对的顶点间用一块木棒加固,模板的长为______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(x﹣y+z)(x+y﹣z)的正确结果为( )
A. x2﹣y2+2xy﹣z2 B. x2﹣2xy+y2﹣z2
C. x2+2xy+y2﹣z2 D. x2+y2﹣2xy+z2
相关试题

