【题目】我们自从有了用字母表示数,发现表达有关的数和数量关系更加简洁明了,从而更助于我们发现更多有趣的结论,请你按要求试一试。
(1)用代数式表示:
①a与b的差的平方;②a与b两数平方和与a、b两数积的2倍的差;
(2)当a=3,b=-2时,求第(1)题中①②所列的代数式的值;
(3)由第(2)题的结果,你发现了什么等式?
(4)利用你发现的结论:求20182-4036×2017+20172的值.
参考答案:
【答案】(1)①(a-b)2;②a2+b2-2ab;(2)当a=3,b=-2时,(a-b)2=![]() 25;(3)(a-b)2=a2+b2-2ab;(4)1.
25;(3)(a-b)2=a2+b2-2ab;(4)1.
【解析】
(1)根据a、b的关系分别列式即可;
(2)把a、b的值代入代数式进行计算即可得解;
(3)根据计算结果相等写出等式;
(4)利用(3)的等式进行计算即可得解.
解:(1)①(a-b)2;②a2+b2-2ab;
(2)当a=3,b=-2时,(a-b)2=![]() 25;
25;
a2+b2-2ab=9+4-2![]() 25;
25;
(3)(a-b)2=a2+b2-2ab;
(4)20182-4036×2017+20172=20182-2×2018×2017+20172=(2018-2017)2=1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着互联网的发展,农副产品也可以网上销售经过一段时间的精准帮扶,小张也建起了自家的网络商店(简称网店),他应用网店将种植的苹果和桃子销往全国各地.其中苹果每箱
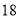 个
个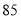 以上的
以上的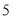 公斤左右包邮
公斤左右包邮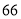 元;桃子每箱
元;桃子每箱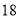 个
个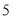 公斤左右包邮
公斤左右包邮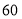 元.请你回答下列问题:
元.请你回答下列问题:(1)网购一箱苹果和一箱桃子共应支付___________元;
(2)某社区重阳节慰问困难居民,计划在这家网店购买
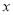 箱苹果和
箱苹果和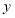 箱桃子,应支付的费用可表示为______________________元;
箱桃子,应支付的费用可表示为______________________元;(3)因为水果不耐贮存,小丽和两个同学合起来在这家网店购买了两箱苹果和一箱桃子,然后平均分配,小丽需支付多钱?她可以分到几个苹果和几个桃子?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在草莓上市的旺季,小颖和妈妈周末计划去草莓园采摘草莓.甲、乙两家草莓园生产的草莓品质相同,每千克售价均为
 元.甲草莓园的优惠方案是:游客进园需购买每人
元.甲草莓园的优惠方案是:游客进园需购买每人 元的门票,采摘的草莓按六折收费;乙草莓园的优惠方案是:游客进园不需购买门票,采摘的草莓超过
元的门票,采摘的草莓按六折收费;乙草莓园的优惠方案是:游客进园不需购买门票,采摘的草莓超过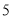 千克后,超过部分按五折收费.请你回答下列问题:
千克后,超过部分按五折收费.请你回答下列问题:(1)如果去乙草莓园采摘
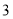 千克草莓,需支付多少元?
千克草莓,需支付多少元?(2)如果
 个人去甲草莓园采摘
个人去甲草莓园采摘 千克草莓,需支付多少元?
千克草莓,需支付多少元?(3)小颖和妈妈准备采摘
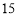 千克草莓送给朋友,哪家会更便宜?请说明理由.
千克草莓送给朋友,哪家会更便宜?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
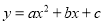 .
.(Ⅰ)若抛物线的顶点为
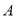 (-2,-4),抛物线经过点
(-2,-4),抛物线经过点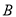 (-4,0).
(-4,0).①求该抛物线的解析式;
②连接
 ,把
,把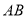 所在直线沿
所在直线沿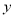 轴向上平移,使它经过原点
轴向上平移,使它经过原点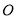 ,得到直线
,得到直线 ,点
,点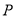 是直线
是直线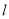 上一动点.
上一动点.设以点
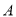 ,
, 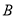 ,
, 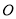 ,
, 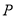 为顶点的四边形的面积为
为顶点的四边形的面积为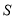 ,点
,点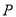 的横坐标为
的横坐标为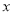 ,当
,当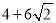 ≤
≤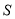 ≤
≤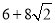 时,求
时,求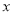 的取值范围;
的取值范围;(Ⅱ)若
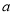 >0,
>0,  >1,当
>1,当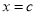 时,
时, 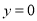 ,当0<
,当0<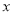 <
<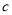 时,
时, 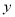 >0,试比较
>0,试比较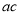 与1的大小,并说明理由.
与1的大小,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】若a、b互为相反数,b、c互为倒数,并且m的立方等于它本身。
(1)求
 +ac值.
+ac值.(2)若a>1,且m<0,S=|2a-3b|-2|b-m|-|b+
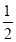 |,求2a-S的值.
|,求2a-S的值.(3)若m≠0,试讨论:x为有理数时|x+m|-|x-m|是否存在最大值?若存在求出这个最大值;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△AOB是直角三角形,∠AOB=90°,OB=2OA,点A在反比例函数y=
 的图象上.若点B在反比例函数y=
的图象上.若点B在反比例函数y=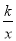 的图象上,则k的值为( )
的图象上,则k的值为( )
A.-4 B.4 C.-2 D.2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在四边形ABCD中,如果对角线AC和BD相交并且相等,那么我们把这样的四边形称为等角线四边形.

(1)在“平行四边形、矩形、菱形,正方形”中, 一定是等角线四边形(填写图形名称);
(2)若M、N、P、Q分别是等角线四边形ABCD四边AB、BC、CD、DA的中点,当对角线AC、BD还要满足 时,四边形MNPQ是正方形;
(3)如图2,已知△ABC中,∠ABC=90°,AB=4,BC=3,D为平面内一点.若四边形ABCD是等角线四边形,且AD=BD,求四边形ABCD的面积.
相关试题

