【题目】有一块直角三角形纸片,两直角边AC=3cm,BC=4cm,现将直角边AC沿直线AD折叠,使它恰好落在斜边AB上,且与AE重合,求CD的长. 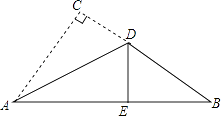
参考答案:
【答案】解:∵有一块直角三角形纸片两直角边AC=3cm,BC=4cm, ∴AB=5cm,
∵将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,
∴DE=CD,AC=AE=3cm,∠DEB=90°,
设CD=xcm,则BD=(4﹣x)cm,
故DE2+BE2=BD2 ,
即x2+(5﹣3)2=(4﹣x)2 ,
解得:x= ![]() ,
,
则CD的长为 ![]() cm
cm
【解析】利用翻折变换的性质得出DE=CD,AC=AE=3cm,∠DEB=90°,进而利用勾股定理得出x的值.
【考点精析】本题主要考查了翻折变换(折叠问题)的相关知识点,需要掌握折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=a(x﹣m)2+n与y轴交于点A,它的顶点为点B,点A、B关于原点O的对称点分别为C、D.若A、B、C、D中任何三点都不在一直线上,则称四边形ABCD为抛物线的伴随四边形,直线AB为抛物线的伴随直线.
(1)如图1,求抛物线y=(x﹣2)2+1的伴随直线的解析式.
(2)如图2,若抛物线y=a(x﹣m)2+n(m>0)的伴随直线是y=x﹣3,伴随四边形的面积为12,求此抛物线的解析式.
(3)如图3,若抛物线y=a(x﹣m)2+n的伴随直线是y=﹣2x+b(b>0),且伴随四边形ABCD是矩形.

①用含b的代数式表示m、n的值;
②在抛物线的对称轴上是否存在点P,使得△PBD是一个等腰三角形?若存在,请直接写出点P的坐标(用含b的代数式表示);若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂承担了加工2100个机器零件的任务,甲车间单独加工了900个零件后,由于任务紧急,要求乙车间与甲车间同时加工,结果比原计划提前12天完成任务.已知乙车间的工作效率是甲车间的1.5倍,求甲、乙两车间每天加工零件各多少个?
-
科目: 来源: 题型:
查看答案和解析>>【题目】规定※是一种新的运算符号,且a※b=ab+a+b,例如:2※3=2×3+2+3=11,那么(3※4)※1=( )
A.19
B.29
C.39
D.49 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=x2+2mx+m与x轴只有一个交点,那么实数m的值为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】鲜花饼是云南的特色小吃,也是中国四大月饼流派滇式月饼的经典代表之一,深受人们喜爱.现某车间要为鲜花饼制作长方体包装盒,已知一个盒子由一个盒身和两个盒底构成,每一张纸板可以做盒身10个或盒底30个.现有纸板100张,应用多少张制作盒身,多少张制作盒底,才能使盒身和盒底正好配套?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A,B,C是数轴上三点,O为原点,点C对应的数为3,BC=2,AB=6.
(1)求点A,B对应的数;
(2)动点M,N分别同时从AC出发,分别以每秒3个单位和1个单位的速度沿数轴正方向运动.P为AM的中点,Q在CN上,且CQ=
 CN,设运动时间为t(t > 0).
CN,设运动时间为t(t > 0).①求点P,Q对应的数(用含t的式子表示);
②t为何值时OP=BQ.

相关试题

