【题目】在某张三角形纸片上,取其一边的中点,沿着过这点的两条中位线分别剪去两个三角形,剩下的部分就是如图所示的四边形;经测量这个四边形的相邻两边长为10cm,6cm,一条对角线的长为8cm;则原三角形纸片的周长是_______.
![]()
参考答案:
【答案】48cm或(32+8![]() )cm
)cm
【解析】分析: 首先补全三角形进而利用平行四边形的性质得出各边长进而得出答案,解答本题应分两种情况进行.
详解: 如图1:
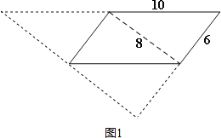
周长为:2×(10+8+6)=48(cm);
如图2:

∵BD=6,BC=8,CD=10,
∴BD2+BC2=CD2,
∴△BCD是直角三角形,
∴∴ACB=∠CBD=90°,
在Rt△ABC中,由勾股定理得,
AB=![]() ,
,
∴周长为2×(10+4![]() +6)=(32+8
+6)=(32+8![]() )(cm);
)(cm);
综上所述:原三角形纸片的周长是48或(32+8![]() )cm.
)cm.
故答案为:48或(32+8![]() )cm.
)cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,
 ,
, 的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,
的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点, ,垂足为G,若
,垂足为G,若 ,则AE的边长为
,则AE的边长为


A.
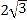 B.
B.  C. 4 D. 8
C. 4 D. 8 -
科目: 来源: 题型:
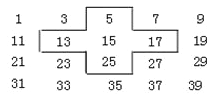
查看答案和解析>>【题目】将连续的奇数1,3,5,7,9…排成如下的数表:
(1)十字框中的五个数的平均数与15有什么关系?
(2)若将十字框上下左右平移,可框住另外的五个数,这五个数的和能等于315吗?若能,请求出这五个数;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A1(1,
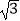 )在直线l1:y=
)在直线l1:y= 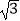 x上,过点A1作A1B1⊥l1交直线l2:y=
x上,过点A1作A1B1⊥l1交直线l2:y= 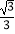 x于点B1 , A1B1为边在△OA1B1外侧作等边三角形A1B1C1 , 再过点C1作A2B2⊥l1 , 分别交直线l1和l2于A2 , B2两点,以A2B2为边在△OA2B2外侧作等边三角形A2B2C2 , …按此规律进行下去,则第n个等边三角形AnBnCn的面积为 . (用含n的代数式表示)
x于点B1 , A1B1为边在△OA1B1外侧作等边三角形A1B1C1 , 再过点C1作A2B2⊥l1 , 分别交直线l1和l2于A2 , B2两点,以A2B2为边在△OA2B2外侧作等边三角形A2B2C2 , …按此规律进行下去,则第n个等边三角形AnBnCn的面积为 . (用含n的代数式表示)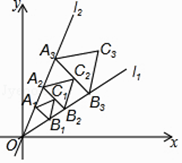
-
科目: 来源: 题型:
查看答案和解析>>【题目】一列火车匀速行驶,经过一条长300米的隧道需要20秒的时间.隧道的顶上有一盏灯,垂直向下发光,灯光照在火车上的时间是10秒.求这列火车的长度.
小冉根据学习解决应用问题的经验对上面问题进行了探究,下面是小冉的探究过程,请补充完成:
设这列火车的长度是x米,那么
(1)从车头经过灯下到车尾经过灯下,火车所走的路程是 米,这段时间内火车的平均速度是 米/秒;
(2)从车头进入隧道到车尾离开隧道,火车所走的路程是 米,这段时间内火车的平均速度是 米/秒;
(3)火车经过灯下和火车通过隧道的平均速度的关系是 ;
(4)由此可以列出方程并求解出这列火车的长度(请列方程求解)
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:(
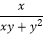 ﹣
﹣ 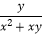 )÷(1﹣
)÷(1﹣ 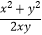 ),其中x=(
),其中x=(  )﹣1﹣(2017﹣
)﹣1﹣(2017﹣  )0 , y=
)0 , y= 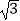 sin60°.
sin60°. -
科目: 来源: 题型:
查看答案和解析>>【题目】为打造徐州故黄河风光带,一段长为360米的河道整治任务交由甲、乙两个工程队接力完成,共用时20天.已知甲队每天整治24米,乙队每天整治16米.
(1)根据题意,小明、小丽分别列出如下的一元一次方程(尚不完整):
小明:24x+16 =360.
小丽:
 .
.请分别指出上述方程中x的意义,并补全方程:
小明:x表示: ;
小丽:x表示: .
(2)求甲、乙两队分别整治河道多少米?(写出完整的解答过程)
相关试题

