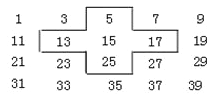
【题目】将连续的奇数1,3,5,7,9…排成如下的数表:
(1)十字框中的五个数的平均数与15有什么关系?
(2)若将十字框上下左右平移,可框住另外的五个数,这五个数的和能等于315吗?若能,请求出这五个数;若不能,请说明理由.
参考答案:
【答案】(1)相等.(2)能.理由见解析
【解析】试题分析:(1)算出十字框中的五个数的平均数,然后判断与15的关系即可;
(2)设中间的数是x,用x表示出其余4个数,然后列出方程并求解即可.
试题解析:(1)相等.
(5+13+15+17+25)÷5=15,
故十字框中的五个数的平均数等于15;
(2)能.
设中间的数是x,则其余4个数分别为x﹣10,x﹣2,x+2,x+10,
则这五个数的和=x﹣10+x﹣2+x+x+2+x+10=5x,
5x=315,
解得,x=63,
由图可知,63排在最左边的第二列,所以,可能成为十字框最中间的一个数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,平面直角坐标系中,直线AB:y=﹣
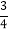 x+b交x轴于点A(8,0),交y轴正半轴于点B.
x+b交x轴于点A(8,0),交y轴正半轴于点B.(1)求点B的坐标;
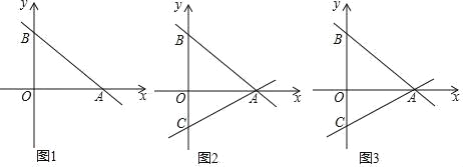
(2)如图2,直线AC交y轴负半轴于点C,AB=BC,P为线段AB上一点,过点P作y轴的平行线交直线AC于点Q,设点P的横坐标为t,线段PQ的长为d,求d与t之间的函数关系式;
(3)在(2)的条件下,M为CA延长线上一点,且AM=CQ,在直线AC上方的直线AB上是否存在点N,使△QMN是以QM为斜边的等腰直角三角形?若存在,请求出点N的坐标及PN的长度;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形纸片ABCD中,AD=8,AB=6,E是边BC上的点,将纸片沿AE折叠,使点B落在点F处,连接FC,当△EFC为直角三角形时,BE的长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,
 ,
, 的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,
的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点, ,垂足为G,若
,垂足为G,若 ,则AE的边长为
,则AE的边长为


A.
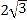 B.
B.  C. 4 D. 8
C. 4 D. 8 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A1(1,
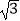 )在直线l1:y=
)在直线l1:y= 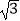 x上,过点A1作A1B1⊥l1交直线l2:y=
x上,过点A1作A1B1⊥l1交直线l2:y= 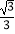 x于点B1 , A1B1为边在△OA1B1外侧作等边三角形A1B1C1 , 再过点C1作A2B2⊥l1 , 分别交直线l1和l2于A2 , B2两点,以A2B2为边在△OA2B2外侧作等边三角形A2B2C2 , …按此规律进行下去,则第n个等边三角形AnBnCn的面积为 . (用含n的代数式表示)
x于点B1 , A1B1为边在△OA1B1外侧作等边三角形A1B1C1 , 再过点C1作A2B2⊥l1 , 分别交直线l1和l2于A2 , B2两点,以A2B2为边在△OA2B2外侧作等边三角形A2B2C2 , …按此规律进行下去,则第n个等边三角形AnBnCn的面积为 . (用含n的代数式表示)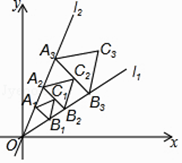
-
科目: 来源: 题型:
查看答案和解析>>【题目】在某张三角形纸片上,取其一边的中点,沿着过这点的两条中位线分别剪去两个三角形,剩下的部分就是如图所示的四边形;经测量这个四边形的相邻两边长为10cm,6cm,一条对角线的长为8cm;则原三角形纸片的周长是_______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一列火车匀速行驶,经过一条长300米的隧道需要20秒的时间.隧道的顶上有一盏灯,垂直向下发光,灯光照在火车上的时间是10秒.求这列火车的长度.
小冉根据学习解决应用问题的经验对上面问题进行了探究,下面是小冉的探究过程,请补充完成:
设这列火车的长度是x米,那么
(1)从车头经过灯下到车尾经过灯下,火车所走的路程是 米,这段时间内火车的平均速度是 米/秒;
(2)从车头进入隧道到车尾离开隧道,火车所走的路程是 米,这段时间内火车的平均速度是 米/秒;
(3)火车经过灯下和火车通过隧道的平均速度的关系是 ;
(4)由此可以列出方程并求解出这列火车的长度(请列方程求解)
相关试题

