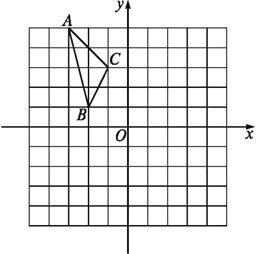
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-3,5),B(-2,1),C(-1,3).
(1)画出△ABC经过平移后得到的△A1B1C1,已知点C1的坐标为(4,0),并写出顶点B1的坐标;
(2)若△ABC和△A2B2C2关于原点O成中心对称,画出△A2B2C2 ,写出顶点B2的坐标;
(3)将△ABC绕着点O按顺时针方向旋转90°得到△A3B3C3,,画出图形并写出△A3B3C3顶点B3的坐标.
参考答案:
【答案】见解析
【解析】分析:(1)由点C平移到点C1得到平移的方法;(2)分别画出点A,B,C关于原点的对称点A2,B2,C2;(3)根据旋转的性质分别画出点A,B,C绕着点O按顺时针方向旋转90°后的点A3,B3,C3.
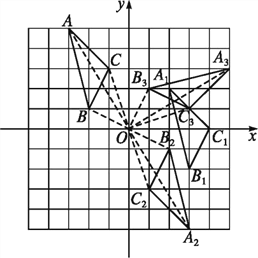
详解:(1)如图,△A1B1C1为所求三角形.因为点C(-1,3)平移后的对应点C1的坐标为(4,0),所以△ABC先向右平移5个单位,再向下平移3个单位得到△A1B1C1,,点B1的坐标为(3,-2).
(2)如图,因为△ABC和△A2B2C2关于原点O成中心对称图形,所以B2(2,-1),.
(3)如图,△A3B3C3为所求三角形,B3(1,2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A,B是数轴上的点,且点A表示数-3,请参照图并思考,完成下列各题:
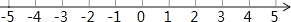
(1)将A点向右移动4个单位长度,那么终点B表示的数是 ,此时 A,B两点间的距离是 .
(2)若把数轴绕点A对折,则对折后,点B落在数轴上的位置所表示的数为 .
(3)若(1)中点B以每秒2个单位长度沿数轴向左运动,A不动,多长时间后,点B与点A距离为2个单位长度?试列式计算.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们规定:有理数xA用数轴上点A表示,xA叫做点A在数轴上的坐标;有理数xB用数轴上点B表示,xB叫做点B在数轴上的坐标.|AB|表示数轴上的两点A,B之间的距离.
(1)借助数轴,完成下表:
xA
xB
xA﹣xB
|AB|
3
2
1
1
1
5
2
﹣3
﹣4
1
﹣5
﹣2
﹣3
﹣6
(2)观察(1)中的表格内容,猜想|AB|= ;(用含xA,xB的式子表示,不用说理)
(3)已知点A在数轴上的坐标是﹣2,且|AB|=8,利用(2)中的结论求点B在数轴上的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(﹣37)﹣(﹣47) (2)10﹣(﹣5)+(﹣9)+6.
(3))-7+13-6+20 (4)0.125+3
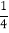 -(+3
-(+3 )+(﹣0.25)
)+(﹣0.25)(5)﹣|﹣1|+|
 ﹣
﹣ |+(﹣2).
|+(﹣2).(6)1+(﹣2)+3+(﹣4)+…+2017+(﹣2018)+2019+(﹣2020)
(7)(﹣5
 )+(﹣9
)+(﹣9 )+17
)+17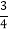 +(﹣3
+(﹣3 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知 m≥2,n≥2,且 m、n 均为正整数,如果将 mn 进行如图所示的“分解”,那么下列四个叙述中正确的有( )
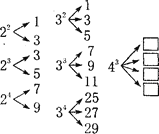
①在 25 的“分解”结果是 15和17两个数.
②在 42 的“分解”结果中最大的数是9.
③若 m3 的“分解”结果中最小的数是 23,则 m=5.
④若 3n 的“分解”结果中最小的数是 79,则 n=5.
A. 1 个 B. 2 个 C. 3 个 D. 4 个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD中,E,F是对角线BD上的两点,如果添加一个条件,使△ABE≌△CDF,则添加的条件不能为( )

A. BE=DF B. BF=DE C. AE=CF D. ∠1=∠2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰直角△ABC中,∠ACB=90°,O是斜边AB的中点,点D,E分别在直角边AC,BC上,且∠DOE=90°,DE交OC于点P,则下列结论:①图形中全等的三角形只有两对;②△ABC的面积等于四边形CDOE的面积的两倍;③CD+CE=
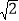 OA;④AD2+BE2=DE2.其中正确的结论有( )
OA;④AD2+BE2=DE2.其中正确的结论有( )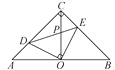
A. 1个 B. 2个 C. 3个 D. 4个
相关试题

