【题目】如图,在等腰直角△ABC中,∠ACB=90°,O是斜边AB的中点,点D,E分别在直角边AC,BC上,且∠DOE=90°,DE交OC于点P,则下列结论:①图形中全等的三角形只有两对;②△ABC的面积等于四边形CDOE的面积的两倍;③CD+CE=![]() OA;④AD2+BE2=DE2.其中正确的结论有( )
OA;④AD2+BE2=DE2.其中正确的结论有( )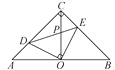
A. 1个 B. 2个 C. 3个 D. 4个
参考答案:
【答案】C
【解析】分析:结论(1)错误.因为图中全等的三角形有3对;结论(2)正确.由全等三角形的性质可以判断;结论(3)正确.利用全等三角形和等腰直角三角形的性质可以判断.结论(4)正确.利用全等三角形的性质以及直角三角形的勾股定理进行判断.
详解:结论(1)错误.理由如下:
图中全等的三角形有3对,分别为△AOC≌△BOC,△AOD≌△COE,△COD≌△BOE.
由等腰直角三角形的性质,可知OA=OC=OB,易得△AOC≌△BOC.
∵OC⊥AB,OD⊥OE,∴∠AOD=∠COE.∴△AOD≌△COE(ASA).
同理可证:△COD≌△BOE.
结论(2)正确.理由如下: ∵△AOD≌△COE,
∴S△AOD=S△COE, ∴S四边形CDOE=S△COD+S△COE=S△COD+S△AOD=S△AOC=![]() S△ABC,
S△ABC,
即△ABC的面积等于四边形CDOE的面积的2倍.
结论(3)正确,理由如下: ∵△AOD≌△COE,∴CE=AD,
∴CD+CE=CD+AD=AC=![]() OA.
OA.
结论(4)正确,理由如下: ∵△AOD≌△COE,∴AD=CE;∵△COD≌△BOE,∴BE=CD.
在Rt△CDE中,由勾股定理得:![]() ,∴
,∴![]() .
.
故本题选C.
-
科目: 来源: 题型:
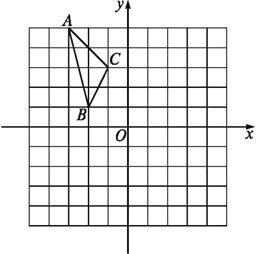
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-3,5),B(-2,1),C(-1,3).
(1)画出△ABC经过平移后得到的△A1B1C1,已知点C1的坐标为(4,0),并写出顶点B1的坐标;
(2)若△ABC和△A2B2C2关于原点O成中心对称,画出△A2B2C2 ,写出顶点B2的坐标;
(3)将△ABC绕着点O按顺时针方向旋转90°得到△A3B3C3,,画出图形并写出△A3B3C3顶点B3的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知 m≥2,n≥2,且 m、n 均为正整数,如果将 mn 进行如图所示的“分解”,那么下列四个叙述中正确的有( )
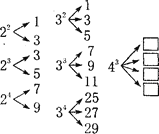
①在 25 的“分解”结果是 15和17两个数.
②在 42 的“分解”结果中最大的数是9.
③若 m3 的“分解”结果中最小的数是 23,则 m=5.
④若 3n 的“分解”结果中最小的数是 79,则 n=5.
A. 1 个 B. 2 个 C. 3 个 D. 4 个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD中,E,F是对角线BD上的两点,如果添加一个条件,使△ABE≌△CDF,则添加的条件不能为( )

A. BE=DF B. BF=DE C. AE=CF D. ∠1=∠2
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,四边形ABCD中,AB=3cm,AD=4cm,BC=13cm,CD=12cm,且∠A=90°,求四边形ABCD的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数填在相应的大括号中:
8,
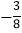 , +2.8, π,
, +2.8, π, 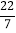 , -0.003, 0,-100, -(-6), -3.626626662…
, -0.003, 0,-100, -(-6), -3.626626662…正数集合{___________________________________________________…}
整数集合{___________________________________________________…}
负分数集合{_________________________________________________…}
无理数集合{_________________________________________________…}.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题:
(1)(-20)-(+3)-(-5) (2)
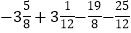
(3) |-3|×(-5)÷(-
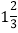 ) (4)
) (4) 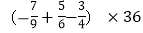
(5)
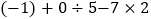 (6)(
(6)(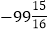 )×4
)×4(7)
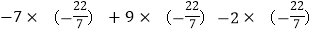 (8)
(8) 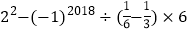
相关试题

