【题目】如图,在正方形ABCD中,点E,N,P,G分别在边AB,BC,CD,DA上,点M,F,Q都在对角线BD上,且四边形MNPQ和AEFG均为正方形,则 ![]() 的值等于 .
的值等于 . 
参考答案:
【答案】![]()
【解析】解:在正方形ABCD中,
∵∠ABD=∠CBD=45°,
∵四边形MNPQ和AEFG均为正方形,
∴∠BEF=∠AEF=90°,∠BMN=∠QMN=90°,
∴△BEF与△BMN是等腰直角三角形,
∴FE=BE=AE= ![]() AB,BM=MN=QM,
AB,BM=MN=QM,
同理DQ=MQ,
∴MN= ![]() BD=
BD= ![]() AB,
AB,
∴ ![]() =
= ![]() =
= ![]() ,
,
所以答案是: ![]() .
.
【考点精析】解答此题的关键在于理解正方形的性质的相关知识,掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为4,点E在BC上,四边形EFGB也是正方形,以B为圆心,BA长为半径画
 ,连结AF,CF,则图中阴影部分面积为 .
,连结AF,CF,则图中阴影部分面积为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】去年某省将地处A、B两地的两所大学合并成了一所综合性大学,为了方便A、B两地师生的交往,学校准备在相距2km的A、B两地之间修筑一条笔直公路(即图中的线段AB),经测量,在A地的北偏东60°方向、B地的西偏北45°方向C处有一个半径为0.7km的公园,问计划修筑的这条公路会不会穿过公园?为什么?(
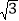 ≈1.732)
≈1.732)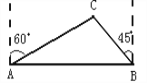
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
 中,
中, 为直线
为直线 上一点,
上一点, 为直线
为直线 上一点,
上一点,


(1)如图1,当
 在
在 上,
上, 在
在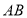 上时,求证
上时,求证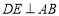 ;
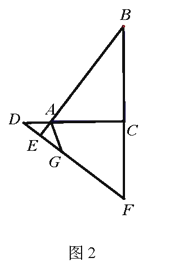
;(2)如图2,当
 在
在 的延长线上,
的延长线上, 在
在 的延长线上时,点
的延长线上时,点 在
在 上,连接
上,连接 ,且
,且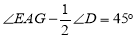 ,求证:
,求证:
(3)如图3,在(2)的条件下,连接
 当
当 平分
平分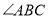 时,将
时,将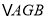 沿着
沿着 折至
折至 探究
探究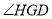 与
与 的数量关系.
的数量关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,点
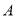 在
在 轴正半轴上,点
轴正半轴上,点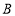 在
在 轴正半轴上连接
轴正半轴上连接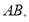
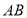 的长为
的长为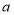 ,其中
,其中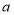 是不等式
是不等式 的最大整数解
的最大整数解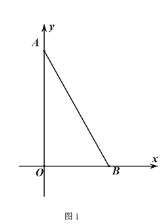
(1)求
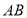 的长
的长(2)动点
 以每秒
以每秒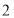 个单位长度的速度在
个单位长度的速度在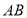 上从
上从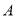 点向
点向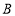 点运动,设
点运动,设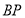 的长度为
的长度为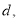 运动时间为
运动时间为 ,请用含
,请用含 的式子表示
的式子表示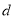 ;
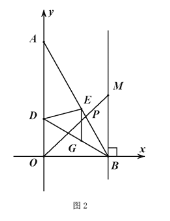
;(3)如图2,在(2)的条件的下,
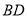 平分
平分 交
交 轴于点
轴于点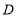 ,点
,点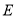 在
在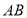 上,点
上,点 在
在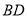 上,连接
上,连接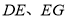 ,且
,且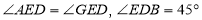 ,点
,点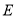 与点
与点 的纵坐标的差为
的纵坐标的差为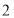 ,连接
,连接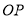 并还延长交过
并还延长交过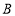 点且与
点且与 轴垂直的直线于
轴垂直的直线于 ,当
,当 为何值时,
为何值时,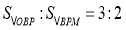 ,并求
,并求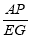 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,甲乙两数学兴趣小组测量出CD的高度,甲小组在地面A处测量,乙小组在上坡B处测量,AB=200m,甲小组测得山顶D的仰角为45°,山坡B处的仰角为30°;乙小组测得山顶D的仰角为58°,求山CD的高度(结果保留一位小数)
参考数据:tan58°≈1.60,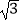 ≈1.732,供选用.
≈1.732,供选用.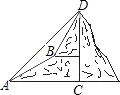
-
科目: 来源: 题型:
查看答案和解析>>【题目】(8分) 小丽想用一块面积为400cm2的正方形纸片,沿着边的方向裁处一块面积为300cm2的长方形纸片.(1)请帮小丽设计一种可行的裁剪方案;
(2)若使长方形的长宽之比为3:2,小丽能用这块纸片裁处符合要求的纸片吗?若能,请帮小丽设计一种裁剪方案,若不能,请简要说明理由.
相关试题

