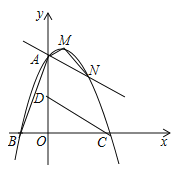
【题目】如图,在直角坐标系中有![]() ,
,![]() 为坐标原点,
为坐标原点,![]() ,将此三角形绕原点
,将此三角形绕原点![]() 顺时针旋转
顺时针旋转![]() ,得到
,得到![]() ,二次函数
,二次函数![]() 的图象刚好经过
的图象刚好经过![]() 三点.
三点.
(1)求二次函数的解析式及顶点![]() 的坐标;
的坐标;
(2)过定点![]() 的直线
的直线![]() 与二次函数图象相交于
与二次函数图象相交于![]() 两点.
两点.
①若![]() ,求
,求![]() 的值;
的值;
②证明:无论![]() 为何值,
为何值,![]() 恒为直角三角形;
恒为直角三角形;
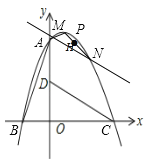
③当直线![]() 绕着定点
绕着定点![]() 旋转时,
旋转时,![]() 外接圆圆心在一条抛物线上运动,直接写出该抛物线的表达式.
外接圆圆心在一条抛物线上运动,直接写出该抛物线的表达式.
参考答案:
【答案】(1)![]() ,
,![]() ;(2)①
;(2)①![]() ;②见解析;③
;②见解析;③![]() .
.
【解析】
(1)求出点A、B、C的坐标分别为(0,3)、(-1,0)、(3,0),即可求解;
(2)①S△PMN=![]() PQ×(x2-x1),则x2-x1=4,即可求解;②k1k2=
PQ×(x2-x1),则x2-x1=4,即可求解;②k1k2=![]() =-1,即可求解;③取MN的中点H,则点H是△PMN外接圆圆心,即可求解.
=-1,即可求解;③取MN的中点H,则点H是△PMN外接圆圆心,即可求解.
(1)![]() ,则
,则![]() ,
,
即点![]() 的坐标分别为
的坐标分别为![]() 、
、![]() 、
、![]() ,
,
则二次函数表达式为:![]() ,
,
即:![]() ,解得:
,解得:![]() ,
,
故函数表达式为:![]() ,
,
点![]() ;
;
(2)将二次函数与直线![]() 的表达式联立并整理得:
的表达式联立并整理得:
![]() ,
,
设点![]() 的坐标为
的坐标为![]() 、
、![]() ,
,
则![]() ,
,
则:![]() ,
,
同理:![]() ,
,
①![]() ,当
,当![]() 时,
时,![]() ,即点
,即点![]() ,
,
![]() ,则
,则![]() ,
,
![]() ,
,
解得:![]() ;
;
②点![]() 的坐标为
的坐标为![]() 、
、![]() 、点
、点![]() ,
,
则直线![]() 表达式中的
表达式中的![]() 值为:
值为:![]() ,直线
,直线![]() 表达式中的
表达式中的![]() 值为:
值为:![]() ,
,
为: ![]() ,
,
故![]() ,
,
即:![]() 恒为直角三角形;
恒为直角三角形;
③取![]() 的中点
的中点![]() ,则点
,则点![]() 是
是![]() 外接圆圆心,
外接圆圆心,
设点![]() 坐标为
坐标为![]() ,
,
则![]() ,
,
![]() ,
,
整理得:![]() ,
,
即:该抛物线的表达式为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c的图象如图,对称轴是直线x=-
 ,有下列结论:(1)ab>0;(2)a+b+c<0;(3)b+2c<0;(4)a-2b+4c>0.其中正确结论的个数是( )
,有下列结论:(1)ab>0;(2)a+b+c<0;(3)b+2c<0;(4)a-2b+4c>0.其中正确结论的个数是( )
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A1,A2,A3,…,An是x轴上的点,且OA1=A1A2=A2A3=A3A4=…=An-1An=1,分别过点A1,A2,A3,…,An作x轴的垂线交二次函数y=
 x2(x>0)的图象于点P1,P2,P3,…,Pn.若记△OA1P1的面积为S1,过点P1作P1B1⊥A2P2于点B1,记△P1B1P2的面积为S2,过点P2作P2B2⊥A3P3于点B2,记△P2B2P3的面积为S3……依次进行下去,最后记△Pn-1Bn-1Pn(n>1)的面积为Sn,则Sn=( )
x2(x>0)的图象于点P1,P2,P3,…,Pn.若记△OA1P1的面积为S1,过点P1作P1B1⊥A2P2于点B1,记△P1B1P2的面积为S2,过点P2作P2B2⊥A3P3于点B2,记△P2B2P3的面积为S3……依次进行下去,最后记△Pn-1Bn-1Pn(n>1)的面积为Sn,则Sn=( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A、B两点,点A在点B左侧,点B的坐标为(1,0)、C(0,﹣3).
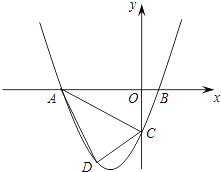
(1)求抛物线的解析式.
(2)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值.
(3)若点E在x轴上,点P在抛物线上,是否存在以A、C、E、P为顶点且以AC为一边的平行四边形?如存在,求点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
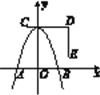
查看答案和解析>>【题目】如图,一条抛物线与x轴相交于A,B两点,其顶点P在折线C-D-E上移动,若点C,D,E的坐标分别为(-1,4),(3,4),(3,1),点B的横坐标的最小值为1,则点A的横坐标的最大值为________.
-
科目: 来源: 题型:
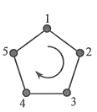
查看答案和解析>>【题目】如图,给正五边形的顶点依次编号 12345,若从某一顶点开始,沿正五边形的边顺时针行走,顶点编号数字是几就走几个边长,则称 这种走法为一次移位,如:小宇在编号为 3 的顶点上时,那么他应该走 3 个边长,即 3-4-5-1 为第一次移位,这时他到达编号为 1 的顶点;然后从 1-2 为第二次移位.若小宇从编号为 2 的顶点开始,第 14 次移位后,则他所处顶点的编号为_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】文美书店决定用不多于20000元购进甲乙两种图书共1200本进行销售.甲、乙两种图书的进价分别为每本20元、14元,甲种图书每本的售价是乙种图书每本售价的1.4倍,若用1680元在文美书店可购买甲种图书的本数比用1400元购买乙种图书的本数少10本.
(1)甲乙两种图书的售价分别为每本多少元?
(2)书店为了让利读者,决定甲种图书售价每本降低3元,乙种图书售价每本降低2元,问书店应如何进货才能获得最大利润?(购进的两种图书全部销售完.)
相关试题

