搜索
【题目】若关于x的一元二次方程(m-2)x2-4x-2=0有两个实数根，则实数m的取值范围是（ ）
A. m≥0B. m>0C. m≥0,m≠2D. m>0,m≠2
参考答案：
【答案】C
【解析】
根据一元二次方程有实数根可以得到其根的判别式大于等于0，据此列出有关m的不等式求的m的取值范围即可，另外还应注意二次项系数为0．
∵关于x的一元二次方程(m-2)x2-4x-2=0有实数根，
∴△≥0，
即：（-4）2-4（m-2）×2≥0，
解得：m≥0，
∵一元二次方程中二次项系数m-2≠0，
∴m≥0且m≠2．
故选C．
-
科目： 来源： 题型：
查看答案和解析>>【题目】问题提出；怎样计算1×2+2×3+3×4+…+（n﹣1）×n呢？
材料学习
计算1+2+3…+n
因为1=
（1×2﹣0×1）；2= （2×3﹣1×2）；3= （3×4﹣2×3）
…，n= [n（n+1）﹣（n﹣1）n]
所以1+2+3+…+n
= （1×2﹣0×1）+ （2×3﹣1×2）+ （3×4﹣2×3）+…+ [n（n+1）﹣（n﹣1）n]
= [1×2﹣0×1+2×3﹣1×2+3×4﹣2×3+…+n（n+1）﹣（n﹣1）n]= n（n+1）
（1）探究应用
观察规律：①1×2=
（1×2×3﹣0×12）；②2×3= （2×3×4﹣1×2×3）；
③3×4= （3×4×5﹣2×3×4）；…
猜想归纳：
根据（1）中观察的规律直接写出：4×5= （）
（n﹣1）×n= []
问题解决：
1×2+2×3+3×4+4×5…+（n﹣1）×n
= （1×2×3﹣0×1×2）+ （2×3×4﹣1×2×3）+ （3×4×5﹣2×3×4）+…+ []
=
（2）拓展延伸
根据上面的规律，请直接写出1×2×3+2×3×4+3×4×5+…+（n﹣2）（n﹣1）n= ． -
科目： 来源： 题型：
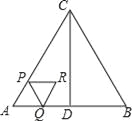
查看答案和解析>>【题目】如图，△ABC是等边三角形，AB=4cm，CD⊥AB于点D，动点P从点A出发，沿AC以2cm/s的速度向终点C运动，当点P出发后，过点P作PQ∥BC交折线AD﹣DC于点Q，以PQ为边作等边三角形PQR，设四边形APRQ与△ACD重叠部分图形的面积为S（cm2），点P运动的时间为t（s）．
（1）当点Q在线段AD上时，用含t的代数式表示QR的长；
（2）求点R运动的路程长；
（3）当点Q在线段AD上时，求S与t之间的函数关系式；
（4）直接写出以点B、Q、R为顶点的三角形是直角三角形时t的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】四边形ABCD中，AD//BC，AD＝BC，则四边形ABCD是_______四边形．
-
科目： 来源： 题型：
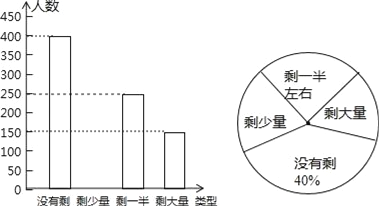
查看答案和解析>>【题目】某高校学生会在食堂发现同学们就餐时剩余饭菜较多，浪费严重，为了让同学们珍惜粮食，养成节约的好习惯，校学生会随机抽查了午餐后部分同学饭菜的剩余情况，并将结果统计后绘制成了如图所示的不完整的统计图．
（1）这次被调查的同学共有 名．
（2）把条形统计图补充完整．
（3）校学生会通过数据分析，估计这次被调查的所有学生一餐浪费的食物可以供200人用一餐．据此估算，该校18000名学生一餐浪费的食物可供多少人食用一餐？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，等边△ABC的边长为6，AD是BC边上的中线，M是AD上的动点，E是AC边上一点，若AE=2，EM+CM的最小值为 ．
-
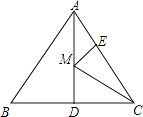
科目： 来源： 题型：
查看答案和解析>>【题目】下列各组数中，数值相等的是（ ）
A. （﹣2）3与﹣23 B. 23与32
C. （﹣3）2与﹣32 D. ﹣（-2）与﹣|﹣2|
相关试题
