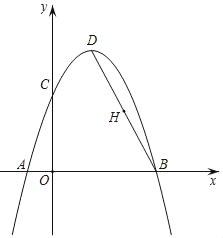
【题目】如图,抛物线y=﹣x2+bx+c经过A(﹣1,0),B(3,0)两点,交y轴于点C,点D为抛物线的顶点,连接BD,点H为BD的中点.请解答下列问题:
(1)求抛物线的解析式及顶点D的坐标;
(2)在y轴上找一点P,使PD+PH的值最小,则PD+PH的最小值为 .
(注:抛物线y=ax2+bx+c(a≠0)的对称轴是直线x=﹣![]() ,顶点坐标为(﹣
,顶点坐标为(﹣![]() ,
,![]() )
)
参考答案:
【答案】(1)函数的解析式为:y=﹣x2+2x+3,顶点D(1,4);(2)![]() .
.
【解析】
先利用待定系数法求出函数的解析式,再连接H′D与y轴交于点P,则PD+PH最小.
(1)∵抛物线y=﹣x2+bx+c过点A(﹣1,0),B(3,0)
∴![]()
解得![]()
∴所求函数的解析式为:y=﹣x2+2x+3
y=﹣x2+2x+3=﹣(x﹣1)2+4
∴顶点D(1,4)
(2)∵B(3,0),D(1,4)
∴中点H的坐标为(2,2)其关于y轴的对称点H′坐标为(﹣2,2)
连接H′D与y轴交于点P,则PD+PH最小
且最小值为:![]() =
=![]()
∴答案:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长方形ABCD中,AB=10厘米,BC=6厘米,点P沿AB边从点A开始向点B以3厘米/秒的速度移动;点Q沿DA边从点D开始向点A以2厘米/秒的速度移动.如果P、Q同时出发,用t (秒)表示移动的时间,那么:
(1)如图1,用含t的代数式表示AP= ,AQ= .并求出当t为何值时线段AP=AQ.
(2)如图2,在不考虑点P的情况下,连接QB,问:当t为何值时△QAB的面积等于长方形面积的
 .
.
-
科目: 来源: 题型:
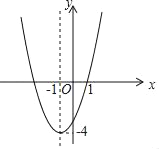
查看答案和解析>>【题目】已知二次函数的图象如图所示.
(1)求这个二次函数的表达式;
(2)将该二次函数图象向上平移 个单位长度后恰好过点(﹣2,0);
(3)观察图象,当﹣2<x<1时,y的取值范围为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°.E、F分别是BC、CD上的点.且∠EAF=60°.探究图中线段BE、EF、FD之间的数量关系.
小王同学探究此问题的方法是,延长FD到点G,使DG=BE.连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是 ;

探索延伸:
如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E、F分别是BC、CD上的点,且∠EAF=
 ∠BAD,上述结论是否仍然成立,并说明理由;
∠BAD,上述结论是否仍然成立,并说明理由;实际应用:
如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东50°的方向以80海里/小时的速度前进1.5小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离?
-
科目: 来源: 题型:
查看答案和解析>>【题目】从﹣2,﹣1,0,1,
 ,4这六个数中,随机抽取一个数记为a,若数a使关于x的分式方程
,4这六个数中,随机抽取一个数记为a,若数a使关于x的分式方程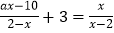 有整数解,且使抛物线y=(a﹣1)x2+3x﹣1的图象与x轴有交点,那么这六个数中所满足条件的a的值之和为( )
有整数解,且使抛物线y=(a﹣1)x2+3x﹣1的图象与x轴有交点,那么这六个数中所满足条件的a的值之和为( )A.
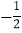 B.
B.  C.
C.  D.
D. 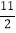
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线y=m(x+3)2+n与y=m(x﹣2)2+n+1交于点A.过点A作x轴的平行线,分别交两条抛物线于点B、C(点B在点C左侧),则线段BC的长为_____.
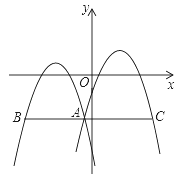
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某小区有一块长为30 m,宽为24 m的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为480 m2,两块绿地之间及周边有宽度相等的人行通道,则人行通道的宽度为________m.
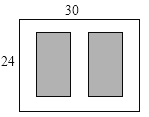
相关试题

