搜索
【题目】计算﹣2a（a2﹣1）的结果是（ ）
A.﹣2a3﹣2a
B.﹣2a3+a
C.﹣2a3+2a
D.﹣a3+2a
参考答案：
【答案】C
【解析】解：原式=﹣2a3+2a， 故选C．
【考点精析】根据题目的已知条件，利用单项式乘多项式的相关知识可以得到问题的答案，需要掌握单项式与多项式相乘，就是根据分配律用单项式去乘多项式的每一项，再把所得的积相加．
-
科目： 来源： 题型：
查看答案和解析>>【题目】点N（x，y）的坐标满足xy＜0，则点N在第______象限．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AC是矩形ABCD的对角线，过AC的中点O作EF⊥AC，交BC于点E，交AD于点F，连接AE，CF．
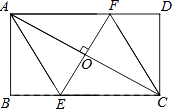
（1）求证：四边形AECF是菱形；
（2）若AB=
，∠DCF=30°，求四边形AECF的面积．（结果保留根号） -
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，借助直角三角板可以找到一元二次方程的实数根．比如对于方程
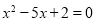，操作步骤是：第一步：根据方程的系数特征，确定一对固定点A（0，1），B（5，2）；
第二步：在坐标平面中移动一个直角三角板，使一条直角边恒过点A，另一条直角边恒过点B；
第三步：在移动过程中，当三角板的直角顶点落在x轴上点C处时，点C的横坐标m即为该方程的一个实数根（如图1）；
第四步：调整三角板直角顶点的位置，当它落在x轴上另一点D处时，点D的横坐标n即为该方程的另一个实数根．
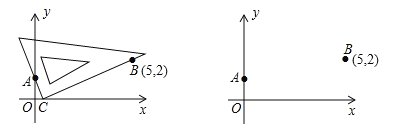
（1）在图2中，按照“第四步”的操作方法作出点D（请保留作出点D时直角三角板两条直角边的痕迹）；
（2）结合图1，请证明“第三步”操作得到的m就是方程
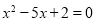的一个实数根；（3）上述操作的关键是确定两个固定点的位置，若要以此方法找到一元二次方程
（a≠0，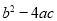
≥0）的实数根，请你直接写出一对固定点的坐标；（4）实际上，（3）中的固定点有无数对，一般地，当m1，n1，m2，n2与a，b，c之间满足怎样的关系时，点P（m1，n1），Q（m2，n2）就是符合要求的一对固定点？
-
科目： 来源： 题型：
查看答案和解析>>【题目】四边形ABCD的四个内角∠A、∠B、∠C、∠D度数之比依次如下，那么其中是平行四边形的是（ ）。
A. 1：2：3：4 B. 2：3：2：3 C. 2：3：3：2 D. 1：3：3：2
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列各点中，在x 轴上的是( ).
A. (3，-3)B. (0，3)C. (-3，0)D. (3，-4)
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，点P(－3，-2019)在：（ ）
A. 第一象限B. 第二象限C. 第三象限D. 第四象限
相关试题
