【题目】已知数轴上A,B两点对应数分别为-2和5,P为数轴上一点,对应数为x.
(1)若P为线段AB的三等分点(把一条线段平均分成相等的三部分的两个点),求P点对应的数.
(2)数轴上是否存在点P,使P点到A点,B点距离和为10?若存在,求出x值;若不存在,请说明理由.
(3)若点A,点B和点P(P点在原点)同时向左运动,它们的速度分别为1,6,3个长度单位/分,则第几分钟时,A,B,P三点中,其中一点是另外两点连成的线段的中点?
参考答案:
【答案】(1) ![]() 或
或![]() ;(2)
;(2) ![]() 或
或![]() ;(3)
;(3) ![]() 或
或![]() 或3
或3
【解析】
(1)先求出AB之间的距离,再根据P点的位置,求出它对应的数.
(2)因分情况进行讨论P点在A点左侧,AB中间和B点右侧三种情况进行讨论.
(3)分三种情况列出方程求出需要的时间.
(1)因数轴上A、B两点对应的数分别是﹣2和5,所以AB=7,又因P为线段AB的三等分点,所以 AP=7÷3=![]() 或AP=7÷3×2=
或AP=7÷3×2=![]() ,所以P点对应的数为
,所以P点对应的数为![]() 或
或![]() ;
;
(2)若P在A点左侧,则﹣2﹣x+5﹣x=10,解得:x=﹣![]() ;
;
若P在A点、B中间.
∵AB=7,∴不存在这样的点P;
若P在B点右侧,则x﹣5+x+2=10,解得:x=![]() ;
;
(3)设第x分钟时,点A的位置为:﹣2﹣x,点B的位置为:5﹣6x,点P的位置为:﹣3x,①当P为AB的中点,则
5﹣6x+(﹣2﹣x)=2×(﹣3x),解得:x=3;
②当A为BP中点时,则
2×(﹣2﹣x)=5﹣6x﹣3x,解得:x=![]() ;
;
③当B为AP中点时,则
2×(5﹣6x)=﹣2﹣x﹣3x,解得:x=![]() .
.
答:第![]() 分钟时,A为BP的中点;第
分钟时,A为BP的中点;第![]() 分钟时,B为AP的中点;第3分钟时,P为AB的中点.
分钟时,B为AP的中点;第3分钟时,P为AB的中点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AD平分∠BAC,DE∥AC交AB于E,DF∥AB交AC于F,若AF=6,则四边形AEDF的周长是( )

A. 24 B. 28 C. 32 D. 36
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合.展开后,折痕DE分别交AB、AC于点E、G.连接GF.下列结论:①∠AGD=112.5°;②AD:AE=2;③S△AGD=S△OGD;④四边形AEFG是菱形;⑤BE=2 OG。其中正确结论的序号是______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】【概念学习】规定:求若干个相同的有理数(均不等于0)的除法运算叫除方,如
 ,
,  等.类比有理数乘方,我们把
等.类比有理数乘方,我们把 记作
记作 ,读作“2的圈3次方”,
,读作“2的圈3次方”,  记作
记作 ,读作“
,读作“ 的圈4次方”.一般地,把
的圈4次方”.一般地,把 (
( ≠0)记作
≠0)记作 ,读作“a的圈c次方”.
,读作“a的圈c次方”.【初步探究】
(1)直接写出计算结果:
 =______________,
=______________,  =______________.
=______________.(2)关于除方,下列说法错误的是( )
A.任何非零数的圈3次方都等于它的倒数 B.对于任何正整数c,
 =1
=1C.
 D.负数的圈奇数次方结果是负数,负数的圈偶数次方结果是正数
D.负数的圈奇数次方结果是负数,负数的圈偶数次方结果是正数【深入思考】
我们知道有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,有理数的除方运算如何转化为乘方运算呢?

 =
= =
=

(1)试一试:仿照上面的算式,将下列运算结果直接写成幂的形式.
 =___________;
=___________;  =_____________;
=_____________;  =____________.
=____________.(2)想一想:将一个非零有理数a的圈c(c≥3)次方写成幂的形式等于___________.
(3)算一算:
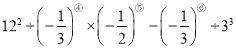
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图:抛物线y=x2﹣1与x轴交于A,B两点,与y轴交于点C.
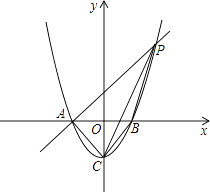
(1)求A,B,C三点的坐标.
(2)过点A作AP∥CB交抛物线于点P,求四边形ACBP的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】解答下列问题:
(1)计算:6÷(-
 +
+ ).
).
方方同学的计算过程如下:原式=6÷(-
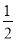 )+6÷
)+6÷ =-12+18=6.
=-12+18=6.请你判断方方同学的计算过程是否正确,若不正确,请你写出正确的计算过程.
(2)请你参考黑板中老师的讲解,用运算律简便计算(请写出具体的解题过程):
①999×(-15);②999×
 +333×(-
+333×(-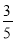 )-999×
)-999×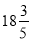 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】“囧”(jiǒng)是一个风靡网络的流行词,像一个人脸郁闷的神情.如图所示,一张边长为8cm的正方形的纸片,剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案(阴影部分).设剪去的小长方形长和宽分别为xcm、ycm,剪去的两个小直角三角形的两直角边长也分别为xcm、ycm.

(1)用含有x、y的代数式表示图中“囧”(阴影部分)的面积.
(2)当x=8,y=2时,求此时“囧”(阴影部分)的面积.
相关试题

