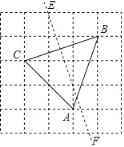
【题目】如图,方格中小正方形的边长为1,△ABC的三个顶点和线段EF的两个端点都在小正方形的格点(顶点)上,小明在观察探究时得到以下四个结论:
①△ABC是等边三角形;②△ABC的周长是![]() ;
;
③△ABC的面积是4;④直线EF是线段BC的垂直平分线.
你认为以上结论中,正确的序号有_____.
参考答案:
【答案】②③④.
【解析】
根据勾股定理求出AC、BC、AB长,即可判断①和②,求出AC边上的高,即可判断③,证△MTD≌△BZC,推出∠ZBC=∠TMD,能求出EF⊥BC,根据等腰三角形性质即可求出CO=BO,即可判断④.
∵由勾股定理得:AB=![]() =
=![]() ,AC=
,AC=![]() =2
=2![]() ,BC=
,BC=![]() =
=![]() ,
,
∴AB=BC,∴△ABC的形状是等腰三角形,∴①错误;
△ABC的周长是![]() +
+![]() +2
+2![]() =2
=2![]() +2
+2![]() ,∴②正确;
,∴②正确;
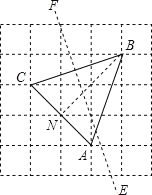
连接BN,由勾股定理得:AN=CN,
在△BCN和△BAN中
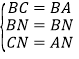 ∴△BCN≌△BAN,
∴△BCN≌△BAN,
∴∠BNC=∠BNA,
∵∠BNC+∠BNA=180![]() ,
,
∴∠BNC=90![]() ,
,
由勾股定理得:BN=![]() =2
=2![]() ,
,
∴△ABC的面积是![]() AC×BN=
AC×BN=![]() ×2
×2![]() ×2
×2![]() =4,∴③正确;
=4,∴③正确;
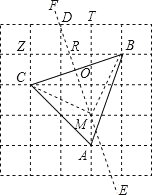
在△MTD和△BZC中
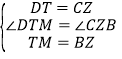 ∴△MTD≌△BZC,
∴△MTD≌△BZC,
∴∠ZBC=∠TMD,
∵∠MTD=90,
∴∠TDM+∠TMD=∠ZBC+∠BRO=90![]() ,
,
∴∠ROB=90![]() ,
,
∴EF⊥BC,
由勾股定理得:BM=CM,
∴CO=BO,即EF是线段BC的垂直平分线,∴④正确;
故答案为:②③④.
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题情境:如图,在Rt△ABC中,∠ACB=90°∠BAC=30°.
动手操作:(1)若以直角边AC所在的直线为对称轴.将Rt△ABC作轴对称变换,请你在原图上作出它的对称图形:
观察发现:(2)Rt△ABC和它的对称图形组成了什么图形?你最准确的判断是 .
合作交流:(3)根据上面的图形,请你猜想直角边BC与斜边AB的数量关系,并证明你的猜想.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CD⊥AB,BE⊥AC,垂足分别为D,E,BE,CD相交于点O,如果AB=AC,那么图中全等的三角形有( )
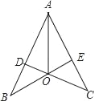
A. 2对 B. 3对 C. 4对 D. 5对
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为25和17,则△EDF的面积为( )

A. 4 B. 5 C. 5.5 D. 6
-
科目: 来源: 题型:
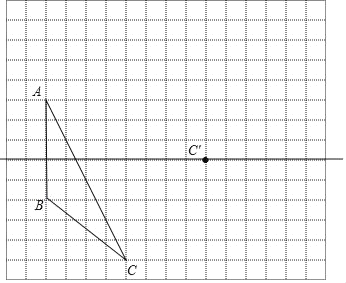
查看答案和解析>>【题目】如图,方格纸中每个小正方形的边长都为1,在方格纸中将三角形ABC经过一次平移后得到三角形A'B' C′,图中标出了点C的对应点C'.
(1)请画出平移后的三角形A'B'C′;
(2)连接AA′,CC′,则这两条线段之间的关系是 ;
(3)三角形A'B'C'的面积为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】每年春季为预防流感,某校利用休息日对教室进行药熏消毒,已知药物燃烧过程及燃烧完后空气中的含药量y(mg/m3)与时间x(h)之间的关系如图所示,根据消毒要求,空气中的含药量不低于3mg/m3且持续时间不能低于10h.请你帮助计算一下,当空气中的含药量不低于3mg/m3时,持续时间可以达到h.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点D在△ABC的边AB上,且∠ACD=∠A.
(1)作∠BDC的平分线DE,交BC于点E.(要求:尺规作图,保留作图痕迹,但不必写出作法);
(2)在(1)的条件下,求证:DE∥AC.

相关试题

