【题目】如图,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB于点E.

(1)求证:△ACD≌△AED;
(2)若∠B=30°,CD=1,求BD的长.
参考答案:
【答案】(1)见解析 (2)2.
【解析】(1)根据角平分线性质求出CD=DE,根据HL定理求出另三角形全等即可;
(2)求出∠DEB=90°,DE=1,根据含30度角的直角三角形性质求出即可.
解答:(1)证明:∵AD平分∠CAB,DE⊥AB,∠C=90°,
∴CD=ED,∠DEA=∠C=90°,
在Rt△ACD和Rt△AED中,
AD=AD,CD=DE,
∴Rt△ACD≌Rt△AED(HL);
(2)解:∵DC=DE=1,DE⊥AB,∴∠DEB=90°,
∵∠B=30°,
∴BD=2DE=2.
“点睛”本题考查了全等三角形的判定,角平分线性质,含30度角的直角三角形性质的应用,注意:角平分线上的点到角两边的距离相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用放大镜看一个三角形,一条边由原来的1 cm变为5 cm,那么看到的图形的高是原来的( )
A. 5倍 B. 15倍 C. 25倍 D. 1倍
-
科目: 来源: 题型:
查看答案和解析>>【题目】某数学兴趣小组研究我国古代《算法统宗》里这样一首诗:我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.诗中后两句的意思是:如果每一间客房住7人,那么有7人无房可住;如果每一间客房住9人,那么就空出一间房.
(1)求该店有客房多少间?房客多少人?
(2)假设店主李三公将客房进行改造后,房间数大大增加.每间客房收费20钱,且每间客房最多入住4人,一次性定客房18间以上(含18间),房费按8折优惠.若诗中“众客”再次一起入住,他们如何订房更合算?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了让市民享受到更多的优惠,某市针对乘坐地铁的人群进行了调查.
(1)为获得乘坐地铁人群的月均花费信息,下列调查方式中比较合理是 ;
A.对某小区的住户进行问卷调查 B.对某班的全体同学进行问卷调查
C.在市里的不同地铁站,对进出地铁的人进行问卷调查
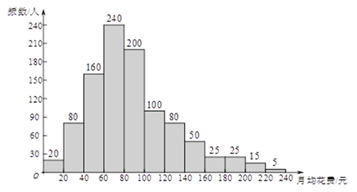
(2)调查小组随机调查了该市1000人上一年乘坐地铁的月均花费(单位:元),绘制了
频数分布直方图,如图所示.
① 根据图中信息,估计平均每人乘坐地铁的月均花费的范围是 元;
A.20—60 B.60—120 C.120—180
②你是用_________(填统计概念)对①进行估计的。
③为了让市民享受到更多的优惠,相关部门拟确定一个折扣线,计划使30%左右的人获得折扣优惠.根据图中信息,乘坐地铁的月均花费达到 元的人可以享受扣.
-
科目: 来源: 题型:
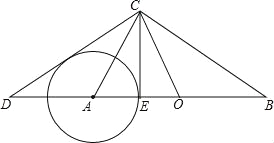
查看答案和解析>>【题目】如图所示,在Rt△ABC与Rt△OCD中,∠ACB=∠DCO=90°,O为AB的中点.
(1)求证:∠B=∠ACD.
(2)已知点E在AB上,且BC2=ABBE.
(i)若tan∠ACD=
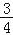 ,BC=10,求CE的长;
,BC=10,求CE的长;(ii)试判定CD与以A为圆心、AE为半径的⊙A的位置关系,并请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=ax+b(a<0)的图象与x的交点坐标是(3,0),那么关于x的方程ax+b=0的解是 , 关于x的不等式ax+b>0的解集是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形中对称轴最多的是( )
A.圆
B.正方形
C.等腰三角形
D.线段
相关试题

