【题目】已知直线y=﹣2x+4与平面直角坐标系中的x轴、y轴分别交于A、B两点,以AB为边作等腰直角三角形ABC,使得点C与原点O在AB两侧,则点C的坐标为_____.
参考答案:
【答案】(6,2)或(4,6)或(3,3)
【解析】
先根据直线的解析式求出A、B两点的坐标,再根据△ABC是等腰直角三角形,则可分三种情况进行讨论:①A为直角顶点;②B为直角顶点;③C为直角顶点.分别求出点C的坐标即可.
解:∵y=-2x+4,
∴y=0时,-2x+4=0,解得x=2,
x=0时,y=4,
∴A(2,0),B(0,4).
以AB为边作等腰直角三角形ABC,使得点C与原点O在AB两侧,可分三种情况:
①当A为直角顶点时,如图,作CD⊥x轴于点D.
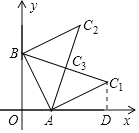
在△ACD和△BAO中,
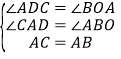 ,
,
∴△ACD≌△BAO(AAS),
∴CD=AO=2,DA=OB=4,
∴OD=OA+AD=2+4=6,
∴C1(6,2);
②当B为直角顶点时,同理可得C2(4,6);
③当C为直角顶点时,显然C3为BC1的中点,则C3(3,3).
综上所述,点C的坐标为(6,2)或(4,6)或(3,3).
故答案为(6,2)或(4,6)或(3,3).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,A(1,2),B(3,1),C(-2,-1).

(1)在图中作出
 关于
关于 轴对称的
轴对称的 .
.(2)写出点
 的坐标(直接写答案).
的坐标(直接写答案).A1_____________,B1______________,C1______________
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学活动课上,某学习小组对有一内角为120°的平行四边形ABCD(∠BAD=120°)进行探究:将一块含60°的直角三角板如图放置在平行四边形ABCD所在平面内旋转,且60°角的顶点始终与点C重合,较短的直角边和斜边所在的两直线分别交线段AB,AD于点E,F(不包括线段的端点).

(1)初步尝试
如图1,若AD=AB,求证:①△BCE≌△ACF,②AE+AF=AC;
(2)类比发现
如图2,若AD=2AB,过点C作CH⊥AD于点H,求证:AE=2FH;
(3)深入探究
如图3,若AD=3AB,探究得: 的值为常数t,则t= .
的值为常数t,则t= . -
科目: 来源: 题型:
查看答案和解析>>【题目】在学习了图形的旋转知识后,数学兴趣小组的同学们又进一步对图形旋转前后的线段之间、角之间的关系进行了探究.

(一)尝试探究
如图1,在四边形ABCD中,AB=AD,∠BAD=60°,∠ABC=∠ADC=90°,点E、F分别在线段BC、CD上,∠EAF=30°,连接EF.
(1)如图2,将△ABE绕点A逆时针旋转60°后得到△A′B′E′(A′B′与AD重合),请直接写出∠E′AF=度,线段BE、EF、FD之间的数量关系为 .
(2)如图3,当点E、F分别在线段BC、CD的延长线上时,其他条件不变,请探究线段BE、EF、FD之间的数量关系,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】爱好思考的小茜在探究两条直线的位置关系查阅资料时,发现了“中垂三角形”,即两条中线互相垂直的三角形称为“中垂三角形”.如图(1)、图(2)、图(3)中,AM、BN是△ABC的中线,AN⊥BN于点P,像△ABC这样的三角形均为“中垂三角形”.设BC=a,AC=b,AB=c.
【特例探究】
(1)如图1,当tan∠PAB=1,c=4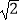 时,a= , b=;
时,a= , b=;
如图2,当∠PAB=30°,c=2时,a= , b=;
(2)【归纳证明】请你观察(1)中的计算结果,猜想a2、b2、c2三者之间的关系,用等式表示出来,并利用图3证明你的结论.
(3)【拓展证明】如图4,ABCD中,E、F分别是AD、BC的三等分点,且AD=3AE,BC=3BF,连接AF、BE、CE,且BE⊥CE于E,AF与BE相交点G,AD=3 ,AB=3,求AF的长.
,AB=3,求AF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
小明遇到这样一个问题:如图1,△ABC中,AB=AC,点D在BC边上,∠DAB=∠ABD,BE⊥AD,垂足为E,求证:BC=2AE.
小明经探究发现,过点A作AF⊥BC,垂足为F,得到∠AFB=∠BEA,从而可证△ABF≌△BAE(如图2),使问题得到解决.
(1)根据阅读材料回答:△ABF与△BAE全等的条件是 AAS(填“SSS”、“SAS”、“ASA”、“AAS”或“HL”中的一个)
参考小明思考问题的方法,解答下列问题:
(2)如图3,△ABC中,AB=AC,∠BAC=90°,D为BC的中点,E为DC的中点,点F在AC的延长线上,且∠CDF=∠EAC,若CF=2,求AB的长;
(3)如图4,△ABC中,AB=AC,∠BAC=120°,点D、E分别在AB、AC边上,且AD=kDB(其中0<k< ),∠AED=∠BCD,求
),∠AED=∠BCD,求  的值(用含k的式子表示).
的值(用含k的式子表示). -
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列一组图形,其中图形①中共有2颗星,图形②中共有6颗星,图形③中共有11颗星,图形④中共有17颗星,…,按此规律,图形⑧中星星的颗数是( )

A.43
B.45
C.51
D.53
相关试题

