【题目】如图,已知 ![]() ,
, ![]() 是直线
是直线 ![]() 上的点,
上的点, ![]() ,过点
,过点 ![]() 作
作 ![]() ,并截取
,并截取 ![]() ,连接
,连接 ![]() ,判断△
,判断△ ![]() 的形状并证明.
的形状并证明.
参考答案:
【答案】解:△CDF是等腰直角三角形.证明如下:
∵AF⊥AD,∠ABC=90°,
∴∠FAD=∠DBC.
在△FAD与△DBC中,∵AD=BC,∠FAD=∠DBC,AF=BD,
∴△FAD≌△DBC(SAS),
∴FD=DC,
∴△CDF是等腰三角形.
∵△FAD≌△DBC,
∴∠FDA=∠DCB.
∵∠BDC+∠DCB=90°,
∴∠BDC+∠FDA=90°,
∴△CDF是等腰直角三角形
【解析】利用SAS证明△FAD≌△DBC可得FD=DC,从而得到△CDF是等腰三角形.再由△FAD≌△DBC,则∠FDA=∠DCB,可证得∠BDC+∠FDA=90°,从而证出△CDF的形状.
【考点精析】本题主要考查了等腰直角三角形的相关知识点,需要掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°才能正确解答此题.
-
科目: 来源: 题型:
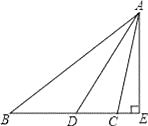
查看答案和解析>>【题目】如图,∠ABC=38°,∠ACB=100°,AD平分∠BAC,AE是BC边上的高,求∠DAE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:12x2﹣3y2= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】x15÷x3等于( )
A.x5
B.x45
C.x12
D.x18 -
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程(m﹣2)x2+2x+1=0有实数根,则m的取值范围是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某小区为了绿化环境,计划分两次购进
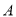 、
、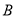 两种花草,第一次分别购进
两种花草,第一次分别购进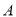 、
、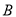 两种花草
两种花草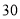 棵和
棵和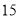 棵,共花费
棵,共花费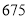 元;第二次分别购进
元;第二次分别购进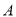 、
、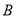 两种花草
两种花草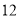 棵和
棵和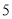 棵.两次共花费
棵.两次共花费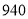 元(两次购进的
元(两次购进的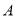 、
、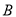 两种花草价格均分别相同).
两种花草价格均分别相同).(
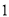 )
)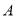 、
、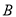 两种花草每棵的价格分别是多少元?
两种花草每棵的价格分别是多少元?(
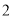 )若购买
)若购买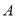 、
、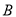 两种花草共
两种花草共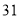 棵,且
棵,且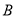 种花草的数量少于
种花草的数量少于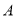 种花草的数量的
种花草的数量的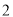 倍,请你给出一种费用最省的方案,并求出该方案所需费用.
倍,请你给出一种费用最省的方案,并求出该方案所需费用. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点
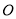 为原点,点
为原点,点 的坐标为
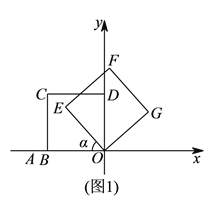
的坐标为 .如图
.如图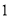 ,正方形
,正方形 的顶点
的顶点 在
在 轴的负半轴上,点
轴的负半轴上,点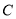 在第二象限.现将正方形
在第二象限.现将正方形 绕点
绕点 顺时针旋转角
顺时针旋转角 得到正方形
得到正方形 .
.

(
 )如图
)如图 ,若
,若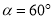 ,
, 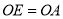 ,求直线
,求直线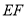 的函数表达式.
的函数表达式.(
 )若
)若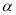 为锐角,
为锐角,  ,当
,当 取得最小值时,求正方形
取得最小值时,求正方形 的面积.
的面积.(
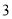 )当正方形
)当正方形 的顶点
的顶点 落在
落在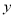 轴上时,直线
轴上时,直线 与直线
与直线 相交于点
相交于点 ,
, 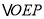 的其中两边之比能否为
的其中两边之比能否为 ?若能,求出
?若能,求出 的坐标;若不能,试说明理由.
的坐标;若不能,试说明理由.
相关试题

