【题目】如图,∠ABC=38°,∠ACB=100°,AD平分∠BAC,AE是BC边上的高,求∠DAE的度数.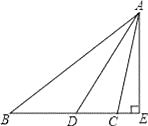
参考答案:
【答案】解:∵∠ABC=38°,∠ACB=100°(己知)
∴∠BAC=180°﹣38°﹣100°=42°(三角形内角和180°).
又∵AD平分∠BAC(己知),
∴∠BAD=21°,
∴∠ADE=∠ABC+∠BAD=59°(三角形的外角性质).
又∵AE是BC边上的高,即∠E=90°,
∴∠DAE=90°﹣59°=31°
【解析】由已知和三角形的内角和可求出∠BAC的度数,再由AD平分∠BAC可得∠BAD的度数,从而求出∠ADE的度数,再在△ABE中求出∠DAE的度数.
【考点精析】根据题目的已知条件,利用三角形的内角和外角和三角形的外角的相关知识可以得到问题的答案,需要掌握三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;三角形一边与另一边的延长线组成的角,叫三角形的外角;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国最新研制的巨型计算机“曙光3000超级服务器”,它的运算峰值可以达到每秒403200000000次,403200000000用科学记数法来表示为 .
-
科目: 来源: 题型:
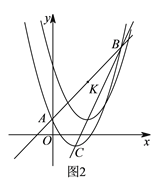
查看答案和解析>>【题目】如图
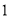 ,二次函数
,二次函数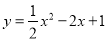 的图象与一次函数
的图象与一次函数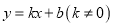 的图象交于
的图象交于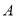 ,
, 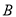 两点,点
两点,点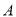 的坐标为
的坐标为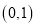 ,点
,点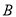 在第一象限内,点
在第一象限内,点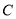 是二次函数图象的顶点,点
是二次函数图象的顶点,点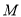 是一次函数
是一次函数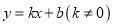 的图象与
的图象与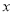 轴的交点,过点
轴的交点,过点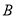 作
作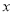 轴的垂线,垂足为
轴的垂线,垂足为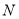 ,且
,且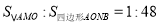 .
. (
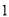 )求直线
)求直线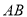 和直线
和直线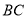 的解析式.
的解析式.(2)点
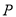 是线段
是线段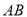 上一点,点
上一点,点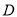 是线段
是线段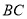 上一点,
上一点, 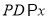 轴,射线
轴,射线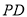 与抛物线交于点
与抛物线交于点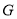 ,过点
,过点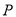 作
作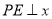 轴于点
轴于点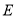 ,
, 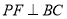 于点
于点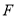 ,当
,当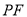 与
与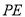 的乘积最大时,在线段
的乘积最大时,在线段 上找一点
上找一点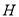 (不与点
(不与点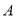 ,点
,点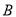 重合),使
重合),使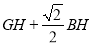 的值最小,求点
的值最小,求点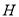 的坐标和
的坐标和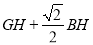 的最小值.
的最小值.(
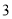 )如图
)如图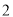 ,直线
,直线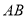 上有一点
上有一点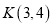 ,将二次函数
,将二次函数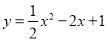 沿直线
沿直线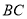 平移,平移的距离是
平移,平移的距离是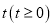 ,平移后抛物线使点
,平移后抛物线使点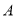 ,点
,点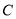 的对应点分别为点
的对应点分别为点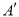 ,点
,点 ;当
;当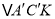 是直角三角形时,求t的值.
是直角三角形时,求t的值.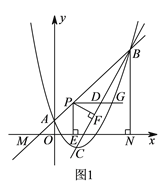
-
科目: 来源: 题型:
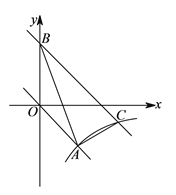
查看答案和解析>>【题目】如图,在平面直角坐标
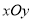 中,正比例函数
中,正比例函数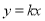 的图象与反比例函数
的图象与反比例函数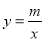 的图象经过点
的图象经过点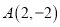 .
.
(
 )分别求这两个函数的表达式.
)分别求这两个函数的表达式.(
 )将直线
)将直线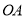 向上平移
向上平移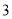 个单位长度后与
个单位长度后与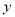 轴交于点
轴交于点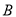 ,与反比例函数图象在第四象限内的交点为
,与反比例函数图象在第四象限内的交点为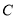 ,连接
,连接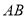 、
、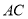 ,求点
,求点 的坐标及
的坐标及 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:12x2﹣3y2= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】x15÷x3等于( )
A.x5
B.x45
C.x12
D.x18 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
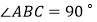 ,
, 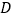 是直线
是直线  上的点,
上的点, 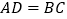 ,过点
,过点 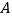 作
作 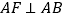 ,并截取
,并截取  ,连接
,连接 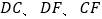 ,判断△
,判断△ 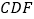 的形状并证明.
的形状并证明.
相关试题

