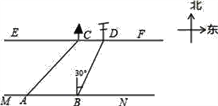
【题目】在综合实践课上,小聪所在小组要测量一条河的宽度,如图,河岸EF∥MN,小聪在河岸MN上点A处用测角仪测得河对岸小树C位于东北方向,然后沿河岸走了30米,到达B处,测得河对岸电线杆D位于北偏东30°方向,此时,其他同学测得CD=10米.请根据这些数据求出河的宽度.(精确到0.1)(参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.132)
≈1.132)
参考答案:
【答案】河的宽度为(30+10![]() )米.
)米.
【解析】如图作BH⊥EF,CK⊥MN,垂足分别为H、K,则四边形BHCK是矩形,设CK=HB=x,根据tan30°=![]() 列出方程即可解决问题.
列出方程即可解决问题.
解:如图作BH⊥EF,CK⊥MN,垂足分别为H、K,则四边形BHCK是矩形,
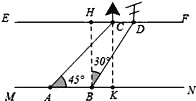
设CK=HB=x,∵∠CKA=90°,∠CAK=45°,∴∠CAK=∠ACK=45°,
∴AK=CK=x,BK=HC=AK﹣AB=x﹣30,∴HD=x﹣30+10=x﹣20,
在RT△BHD中,∵∠BHD=30°,∠HBD=30°,∴tan30°=HD:HB,
∴![]() =
=![]() ,解得x=30+10
,解得x=30+10![]() .∴河的宽度为(30+10
.∴河的宽度为(30+10![]() )米.
)米.
“点睛”本题考查解直角三角形的应用、方向角、三角函数等知识,解题的关键是添加辅助线构造直角三角形,学会利用三角函数的定义,列出方程解决问题,属于中考常考题型.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点(a,2)与点(b,﹣2)关于原点中心对称,则a+b的值是__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】斜边和一条_________对应相等的两个直角三角形全等(可以简写成“________________”或“HL”).
-
科目: 来源: 题型:
查看答案和解析>>【题目】角平分线性质定理的逆定理:角的内部,到_________________的点,在这个角的平分线上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将抛物线C1:y=x2﹣4x+1先向左平移3个单位,再向下平移2个单位得到将抛物线C2,则抛物线C2的解析式为:_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种商品每件的标价为200元,按标价的九折销售时,每件仍能获利20%,则这种商品每件的进价为____元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】﹣2的平方等于( )
A.±4B.2C.﹣4D.4
相关试题

