Question

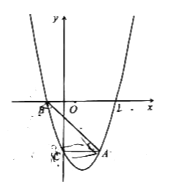
【题目】如图，抛物线经过点，与轴负半轴交于点，与轴交于点，且.

（1）求抛物线的解析式；

（2）点在轴上，且，求点的坐标；

（3）点在抛物线上，点在抛物线的对称轴上，是否存在以点，，，为顶点的四边形是平行四边形？若存在。求出所有符合条件的点的坐标；若不存在，请说明理由.

Answer 1

【答案】（1）y=x2﹣2x﹣3；（2）D1（0，1），D2（0，﹣1）；（3）存在，M（4，5）或（﹣2，5）或（0，﹣3）

【解析】

试题分析：（1）待定系数法即可得到结论；

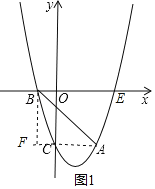
（2）连接AC，作BF⊥AC交AC的延长线于F，根据已知条件得到AF∥x轴，得到F（﹣1，﹣3），设D（0，m），则OD=|m|即可得到结论；

（3）设M（a，a2﹣2a﹣3），N（1，n），①以AB为边，则AB∥MN，AB=MN，如图2，过M作ME⊥对称轴y于E，AF⊥x轴于F，于是得到△ABF≌△NME，证得NE=AF=3，ME=BF=3，得到M（4，5）或（﹣2，5）；②以AB为对角线，BN=AM，BN∥AM，如图3，则N在x轴上，M与C重合，于是得到结论．

试题解析：（1）由y=ax2+bx﹣3得C（0．﹣3），

∴OC=3，

∵OC=3OB，

∴OB=1，

∴B（﹣1，0），

把A（2，﹣3），B（﹣1，0）代入y=ax2+bx﹣3得，

∴，

∴抛物线的解析式为y=x2﹣2x﹣3；

（2）设连接AC，作BF⊥AC交AC的延长线于F，

∵A（2，﹣3），C（0，﹣3），

∴AF∥x轴，

∴F（﹣1，﹣3），

∴BF=3，AF=3，

∴∠BAC=45°，

设D（0，m），则OD=|m|，

∵∠BDO=∠BAC，

∴∠BDO=45°，

∴OD=OB=1，

∴|m|=1，

∴m=±1，

∴D1（0，1），D2（0，﹣1）；

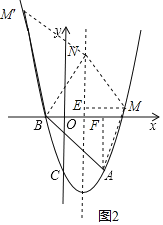
（3）设M（a，a2﹣2a﹣3），N（1，n），

①以AB为边，则AB∥MN，AB=MN，如图2，过M作ME⊥对称轴y于E，AF⊥x轴于F，

则△ABF≌△NME，

∴NE=AF=3，ME=BF=3，

∴|a﹣1|=3，

∴a=4或a=﹣2，

∴M（4，5）或（﹣2，5）；

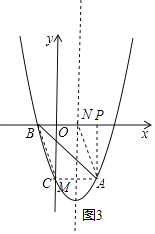
②以AB为对角线，BN=AM，BN∥AM，如图3，

则N在x轴上，M与C重合，

∴M（0，﹣3），

综上所述，存在以点A，B，M，N为顶点的四边形是平行四边形，M（4，5）或（﹣2，5）或（0，﹣3）．