【题目】已知动点P以每秒1cm的速度沿图甲的边框按从BCDEFA的路径移动,相应的△ABP的面积S与时间t之间的关系如图乙中的图象表示.若AB=3cm,试回答下列问题

(1)图甲中的BC长是多少?
(2)图乙中的a是多少?
(3)图甲中的图形面积是多少?
(4)图乙中的b是多少?
参考答案:
【答案】(1)4cm;(2)6cm2;(3)15cm2;(4)17秒
【解析】
(1)根据题意得:动点P在BC上运动的时间是4秒,又由动点的速度,可得BC的长;
(2)由(1)可得BC的长,又由AB=3cm,可以计算出△ABP的面积,即可得到a的值;
(3)分析图形可得,甲中的图形面积等于AB×AF﹣CD×DE,根据图象求出CD,DE,AF的长,代入数据计算可得答案;
(4)计算BC+CD+DE+EF+FA的长度,又由P的速度,计算可得b的值.
解:(1)动点P在BC上运动时,对应的时间为0到4秒,易得:BC=1cm/秒×4秒=4cm;
故图甲中的BC长是4cm.
(2)由(1)可得,BC=4cm,则:a=![]() ×BC×AB=6cm2;
×BC×AB=6cm2;
图乙中的a是6cm2.
(3)由图可得:CD=2×1=2cm,DE=1×3=3cm,
则AF=BC+DE=7cm,又由AB=3cm,
则甲图的面积为AB×AF﹣CD×DE=3×7﹣2×3=15cm2,
图甲中的图形面积为15cm2.
(4)根据题意,动点P共运动了BC+CD+DE+EF+FA=4+2+3+1+7=17cm,
其速度是1cm/秒,则b=![]() =17秒,
=17秒,
图乙中的b是17秒.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校九年级10个班师生举行毕业文艺汇演,每班2个节目,有歌唱与舞蹈两类节目,年级统计后发现歌唱类节目数比舞蹈类节目数的2倍少4个.
(1)九年级师生表演的歌唱与舞蹈类节目数各有多少个?
(2)该校七、八年级师生有小品节目参与,在歌唱、舞蹈、小品三类节目中,每个节目的演出平均用时分别是5分钟、6分钟、8分钟,预计所有演出节目交接用时共花15分钟.若从20:00开始,22:30之前演出结束,问参与的小品类节目最多能有多少个?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)如图,ABCD中,点E,F在直线AC上(点E在F左侧),BE∥DF.

(1)求证:四边形BEDF是平行四边形;
(2)若AB⊥AC,AB=4,BC=
 ,当四边形BEDF为矩形时,求线段AE的长.
,当四边形BEDF为矩形时,求线段AE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知每件
 奖品价格相同,每件
奖品价格相同,每件 奖品价格相同,老师要网购
奖品价格相同,老师要网购 两种奖品
两种奖品 件,若购买
件,若购买 奖品
奖品 件、
件、 奖品
奖品 件,则微信钱包内的钱会差
件,则微信钱包内的钱会差 元;若购买
元;若购买 奖品
奖品 件、
件、 奖品
奖品 件,则微信钱包的钱会剩余
件,则微信钱包的钱会剩余 元,老师实际购买了
元,老师实际购买了 奖品
奖品 件,
件, 奖品
奖品 件,则微信钱包内的钱会剩余__________元.
件,则微信钱包内的钱会剩余__________元. -
科目: 来源: 题型:
查看答案和解析>>【题目】问题提出:若一个四边形的两组对边乘积之和等于它的两条对角线的乘积,则称这个四边形为巧妙四边形.
初步思考:(1)写出你所知道的四边形是巧妙四边形的两种图形的名称: , .
(2)小敏对巧妙四边形进行了研究,发现圆的内接四边形一定是巧妙四边形.
如图①,四边形ABCD是⊙O的内接四边形.
求证:AB·CD+BC·AD=AC·BD.
小敏在解答此题时,利用了“相似三角形”进行证明,她的方法如下:
在BD上取点M,使∠MCB=∠DCA.
(请你在下面的空白处完成小敏的证明过程.)
推广运用:如图②,在四边形ABCD中,∠A=∠C=90°,AD=
 ,AB=
,AB= ,CD=2.求AC的长.
,CD=2.求AC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
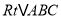 中,
中,  ,
,  ,
, 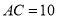 ,
,  和
和 的平分线相交于点E,过点E作
的平分线相交于点E,过点E作 交
交 于点F,那么EF的长为( )
于点F,那么EF的长为( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中,  ,点D, E分别在
,点D, E分别在 上,且
上,且 ,将
,将 沿DE折叠,点C恰好落在AB边上的点F处,如果
沿DE折叠,点C恰好落在AB边上的点F处,如果 ,
, 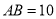 ,那么CD的长为__________.
,那么CD的长为__________.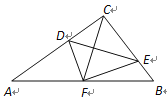
相关试题

