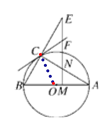
【题目】(如图,⊙O是△ABC的外接圆,圆心O在AB上,且∠B=2∠A,M是OA上一点,过M作AB的垂线交AC于点N,交BC的延长线于点E,直线CF交EN于点F,EF=FC.
(1)求证:CF是⊙O的切线;
(2)若⊙O的半径为2,且AC=CE,求AM的长.

参考答案:
【答案】(1)详见解析;(2)3-![]() .
.
【解析】试题分析:(1)连接OC,如图,根据圆周角定理得到∠ACB=90°,则利用∠B=2∠A可计算出∠B=60°,∠A=30°,易得∠E=30°,接着由EF=FC得到∠ECF=∠E=30°,所以∠FCA=60°,加上∠OCA=∠A=30°,所以∠FCO=∠FCA+∠ACO=90°,于是可根据切线的判定得到FC是⊙O的切线;
(2)利用含30度的直角三角形三边的关系.在Rt△ABC中可计算出![]() ,
,
![]() ,则
,则![]() ,所以BE=BC+CE=
,所以BE=BC+CE=![]() ,然后在Rt△BEM中计算出
,然后在Rt△BEM中计算出![]() 再计算AB-BM的值即可.
再计算AB-BM的值即可.
证明:如图,连接OC.
∵⊙O是△ABC的外接圆,圆心O在AB上,
∴AB是⊙O的直径,
∴∠ACB=90°.
又∵∠B=2∠A,
∴∠B=60°,∠A=30°.
∵EM⊥AB,∴∠EMB=90°.
在Rt△EMB中,∠B=60°,
∴∠E=30°.
又∵EF=FC,
∴∠ECF=∠E=30°.
又∵∠ECA=90°,
∴∠FCA=60°.
∵OA=OC,
∴∠OCA=∠A=30°,
∴∠FCO=∠FCA+∠ACO=90°,
∴OC⊥CF,
∴FC是⊙O的切线;
(2)在Rt△ABC中,∵∠ACB=90°,∠A=30°,AB=4,
∴BC=![]() AB=2,AC=
AB=2,AC=![]() =
=![]() BC=2
BC=2![]() .
.
∵AC=CE,
∴CE=2![]() ,
,
∴BE=BC+CE=2+2![]() .
.
在Rt△BEM中,∠BME=90°,∠E=30°,
∴BM=![]() BE=1+
BE=1+![]() ,
,
∴AM=AB-BM=4-1-![]() =3-
=3-![]() .
.
-
科目: 来源: 题型:
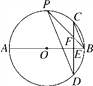
查看答案和解析>>【题目】如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,PB与CD交于点F,∠PBC=∠C.
(1)求证:CB∥PD;
(2)若∠PBC=22.5°,⊙O的半径R=2,求劣弧AC的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等边△ABC和⊙M.
(1)如图l,若⊙M与BA的延长线AK及边AC均相切,求证: AM∥BC;
(2)如图2,若⊙M与BA的延长线AK、BC的延长线CF及边AC均相切,求证:四边形ABCM是平行四边形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在学习了二次根式后,小明同学发现有的二次根式可以写成另一个二次根式的平方的形式.
比如:
 .善于动脑的小明继续探究:
.善于动脑的小明继续探究:当
 为正整数时,若
为正整数时,若 ,则有
,则有 ,所以
,所以 ,
,  .
.请模仿小明的方法探索并解决下列问题:
(1)当
 为正整数时,若
为正整数时,若 ,请用含有
,请用含有 的式子分别表示
的式子分别表示 ,得:
,得:  ,
,  ;
;(2)填空:


-
 ;
;(3)若
 ,且
,且 为正整数,求
为正整数,求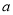 的值.
的值. -
科目: 来源: 题型:
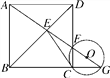
查看答案和解析>>【题目】如图,由正方形ABCD的顶点A引一直线分别交BD、CD及BC的延长线于E、F、G,连接EC.
求证:CE是△CGF的外接圆⊙O的切线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若∠1与∠2是对顶角,∠3与∠2互余,且∠3=40°,那么∠1=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】多项式3a2b﹣2a+3是_____次_____项式.
相关试题

