【题目】如图,在正方形ABCD中,点E在边AD上,点F在边BC的延长线上,连结EF与边CD相交于点G,连结BE与对角线AC相交于点H,AE=CF,BE=EG.
(1)求证:EF∥AC;(2)求∠BEF大小;

参考答案:
【答案】(1)、证明过程见解析;(2)、60°.
【解析】
试题分析:(1)、根据正方形的性质得出AD∥BF,结合AE=CF可得四边形ACFE是平行四边形,从而得出EF∥AC;(2)、连接BG,根据EF∥AC可得∠F=∠ACB=45°,根据∠GCF=90°可得∠CGF=∠F=45°可得CG=CF,根据AE=CF可得AE=CG,从而得出△BAE≌△BCG,即BE=EG,得出△BEG为等边三角形,得出∠BEF的度数.
试题解析:(1)、∵四边形ABCD是正方形 ∴AD∥BF ∵AE=CF ∴四边形ACFE是平行四边形 ∴EF∥AC
(2)、连接BG ∵EF∥AC, ∴∠F=∠ACB=45°, ∵∠GCF=90°, ∴∠CGF=∠F=45°, ∴CG=CF,
∵AE=CF, ∴AE=CG, ∴△BAE≌△BCG(SAS) ∴BE=BG, ∵BE=EG, ∴△BEG是等边三角形,
∴∠BEF=60°
-
科目: 来源: 题型:
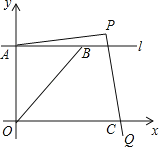
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线l平行x轴,交y轴于点A,第一象限内的点B在l上,连结OB,动点P满足∠APQ=90°,PQ交x轴于点C.
(1)当动点P与点B重合时,若点B的坐标是(2,1),求PA的长.
(2)当动点P在线段OB的延长线上时,若点A的纵坐标与点B的横坐标相等,求PA:PC的值.
(3)在(2)的条件下,已知AB=3,OB:BP=3:1,求四边形AOCP的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若函数y=(m﹣1)x2+3x+1是二次函数,则有( )
A.m≠0
B.m≠1
C.x≠0
D.x≠1 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式中运算错误的是( )
A. 2a﹣a=a B. -(a﹣b)=﹣a+b C. a+a2=a3 D. 2(a+b)=2a+2b
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,△ABC的周长为21cm,AB=6cm,BC边上中线AD=5cm,△ACD周长为16cm,则AC的长为__________cm.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小颖和小红两位同学在学习“概率”时,做投掷骰子(质地均匀的正方体)实验,他们共做了60次实验,实验的结果如下:
(1)计算“3点朝上”的频率和“5点朝上”的频率;
(2)小颖说:“根据上述实验,一次实验中出现5点朝上的概率最大”;小红说:“如果投掷600次,那么出现6点朝上的次数正好是100次”,小颖和小红的说法正确吗?为什么?
朝上的点数
1
2
3
4
5
6
出现的次数
7
9
6
8
20
10
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年5月,池州市杏花村文化旅游景区举办了国际玫瑰灯光节.据不完全统计,当晚约有98000人次来到池州市杏花村文化旅游景区、赏灯.用科学记数法表示98000正确的是( )
A. 9.8×104 B. 9.8×105 C. 98×103 D. 9.8×10-4
相关试题

