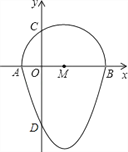
【题目】如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”.已知点A、B、C、D分别是“果圆”与坐标轴的交点,AB为半圆的直径,抛物线的解析式为y=x2﹣2x﹣3,求这个“果圆”被y轴截得的线段CD的长.
参考答案:
【答案】这个“果圆”被y轴截得的线段CD的长3+![]() .
.
【解析】试题分析:连接AC,BC,有抛物线的解析式可求出A,B,C的坐标,进而求出AO,BO,DO的长,在直角三角形ACB中,利用射影定理可求出CO的长,进而可求出CD的长.
试题解析:连接AC,BC,
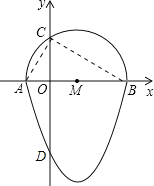
∵抛物线的解析式为y=(x-1)2-4,
∴点D的坐标为(0,3),
∴OD的长为3,
设y=0,则0=(x-1)2-4,
解得:x=1或3,
∴A(1,0),B(3,0)
∴AO=1,BO=3,
∵AB为半圆的直径,
∴∠ACB=90°,
∵CO⊥AB,
∴CO2=AOBO=3,
∴CO=![]() ,
,
∴CD=CO+OD=3+![]() ,
,
故答案为:3+![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算或运算中,正确的是( )
A. a6÷a2=a3B. (﹣2a2)3=﹣8a3
C. (a﹣b)2=a2﹣b2D. (a﹣3)(3+a)=a2﹣9
-
科目: 来源: 题型:
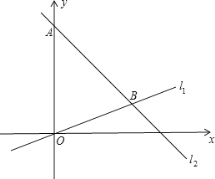
查看答案和解析>>【题目】已知,如图,在平面直角坐标系内,点A的坐标为(0,24 ),经过原点的直线l1与经过点A的直线l2相交于点B,点B坐标为(18,6).
(1)求直线l1,l2的表达式;
(2)点C为线段OB上一动点 (点C不与点O,B重合),作CD∥y轴交直线l2于点D,过点C,D分别向y轴作垂线,垂足分别为F,E,得到矩形CDEF.
①设点C的纵坐标为a,求点D的坐标(用含a的代数式表示);
②若矩形CDEF的面积为60,请直接写出此时点C的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】1 km2的土地上一年内从太阳得到的能量相当于燃烧1.3×108 kg的煤所产生的能量,那么9.6×106 km2的土地上一年内从太阳得到的能量相当于燃烧多少千克的煤?
-
科目: 来源: 题型:
查看答案和解析>>【题目】直角三角形是特殊的三角形,所以不仅可以应用一般三角形判定全等的方法,还有直角三角形特殊的判定方法,即 ________公理.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列等式:
第1个等式:a1=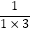 =
=  ×(1﹣
×(1﹣  );
);
第2个等式:a2= =
=  ×(
×(  ﹣
﹣  );
);
第3个等式:a3= =
=  ×(
×(  ﹣
﹣  );
);
第4个等式:a4= =
=  ×(
×(  ﹣
﹣  );
);
…
请解答下列问题:
(1)按以上规律列出第5个等式:a5=;
(2)用含有n的代数式表示第n个等式:an==(n为正整数);
(3)求a1+a2+a3+a4+…+a100的值. -
科目: 来源: 题型:
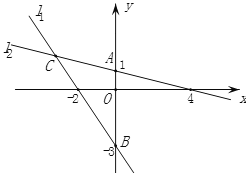
查看答案和解析>>【题目】两个一次函数的图象如图所示,
(1)分别求出两个一次函数的解析式;
(2)求出两个一次函数图象的交点C坐标;
(3)求这两条直线与y轴围成△ABC的面积.
相关试题

