【题目】若顺次连结四边形ABCD各边中点所得四边形是矩形,则原四边形必定是( )
A.正方形
B.对角线相等的四边形
C.菱形
D.对角线相互垂直的四边形
参考答案:
【答案】D
【解析】证明:∵四边形EFGH是矩形, ∴∠FEH=90°,
又∵点E、F、分别是AD、AB、各边的中点,
∴EF是三角形ABD的中位线,
∴EF∥BD,
∴∠FEH=∠OMH=90°,
又∵点E、H分别是AD、CD各边的中点,
∴EH是三角形ACD的中位线,
∴EH∥AC,
∴∠OMH=∠COB=90°,
即AC⊥BD.
故选D.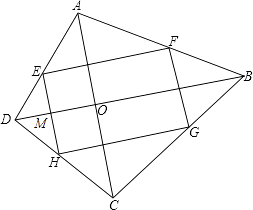
这个四边形ABCD的对角线AC和BD的关系是互相垂直.理由为:根据题意画出相应的图形,如图所示,由四边形EFGH为矩形,根据矩形的四个角为直角得到∠FEH=90°,又EF为三角形ABD的中位线,根据中位线定理得到EF与DB平行,根据两直线平行,同旁内角互补得到∠EMO=90°,同理根据三角形中位线定理得到EH与AC平行,再根据两直线平行,同旁内角互补得到∠AOD=90°,根据垂直定义得到AC与BD垂直.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将正方形ABCO绕点A顺时针旋转一定角度,得到正方形ADEF,ED交线段OC于点G,ED的延长线交线段BC于点P,连AP、AG.
(1)求证:△AOG≌△ADG;
(2)求∠PAG的度数;并判断线段OG、PG、BP之间的数量关系,说明理由;
(3)若正方形ABCO的边长为
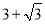 ,∠1=∠2,求AP的长.
,∠1=∠2,求AP的长.
-
科目: 来源: 题型:
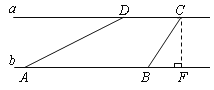
查看答案和解析>>【题目】河流两岸a、b互相平行,C、D是河岸a上间隔50m的两个电线杆.某人在河岸b上的A处测得∠DAB=30°,然后沿河岸走了100m到达B处,测得∠CBF=60°,求河流的宽度CF的值(结果精确到个位).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果等式(x﹣3)2x﹣1=1,则x= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)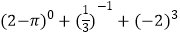
(2)(2a﹣b﹣3)(2a+b﹣3) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是半圆直径,半径OC⊥AB于点O,点D是弧BC的中点,连结CD、AD、OD,给出以下四个结论:①∠DOB=∠ADC;②CE=OE;③△ODE∽△ADO;④2CD2=CE·AB.其中正确结论的序号是( )
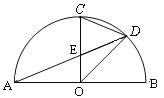
A. ①③ B. ②④ C. ①②③ D. ①④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果用﹣10%表示某商品的出口额比上一年减少10%,那么+12%则表示该商品的出口额比上一年( )
A.减少12%
B.增加12%
C.减少22%
D.增加2%
相关试题

