【题目】如图,在矩形ABCD中,把∠B,∠D分别翻折,使点B,D分别落在对角线AC上的点E,F处,折痕分别为CM,AN.
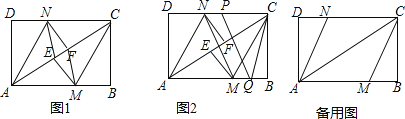
(1)求证:△AND≌△CMB;
(2)连接MF、NE,证明四边形MFNE是平行四边形;四边形MFNE是菱形吗?请说明理由;
(3)点P、Q是矩形的边CD、AB上的两点,连接PQ、CQ、MN,如图2所示,若PQ=CQ,PQ∥MN,且AB=4,BC=3,DN=![]() ,求PC的长度.
,求PC的长度.
参考答案:
【答案】见解析
【解析】
试题分析:(1)根据折叠的性质得出∠DAN=∠NAC,∠BCM=∠ACM,从而根据AD∥BC可得出∠DAN=∠BCM,从而即可判断出△ADN≌△CBM.
(2)连接NE、MF,根据(1)的结论可得出NF=ME,再由∠NFE=∠MEF可判断出NF∥ME,在直角三角形NFE中,NE为斜边,NF为直角边,可判断四边形MFNE不是菱形.
(3)设AC与MN的交点为O,EF=x,作QG⊥PC于G点,首先求出AC=5,根据翻折变换知:AF=CE=3,于是可得AF+(CE﹣EF)=5,可得EF=1,在Rt△NFE中,NO2=NF2+OF2,求出NO的长,即NM=PQ=QC=2NO,PC=2![]() .
.
(1)证明:∵四边形ABCD是正方形,
∴AD=BC,∠B=∠D=90°,
由折叠的性质得出∠DAN=∠NAC,∠BCM=∠ACM,
∵AD∥BC,
∴∠DAC=∠BCA,
∴∠DAN=∠BCM,
在Rt△AND和Rt△CMB中,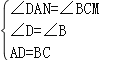 ,
,
∵∴△AND≌△CMB(AAS)
(2)解:由(1)得:△AND≌△CMB,
∴NF=ME,
∵∠NFE=∠MEF,
∴NF∥ME,
∴四边形MFNE是平行四边形,
∵MN与EF不垂直,
∴四边形MFNE不是菱形;
(3)解:设AC与MN的交点为O,EF=x,作QG⊥PC于G点,如图所示:
∵AB=4,BC=3,
∴AC=5,
∵AF=CE=BC=3,
∴2AF﹣EF=AC,即6﹣x=5,
解得:x=1,
∴EF=1,
∴CF=2,
由折叠的性质得:NF=DN=![]() ,
,
∵OE=OF=![]() EF=
EF=![]() ,
,
∴在Rt△NFO中,ON2=OF2+NF2,
∴ON=![]() ,
,
∴MN=2ON=![]() ,
,
∵PQ∥MN,PN∥MQ,
∴四边形MQPN是平行四边形,
∴MN=PQ=![]() ,
,
∵PQ=CQ,
∴△PQC是等腰三角形,
∴PG=CG,
在Rt△QPG中,PG2=PQ2﹣QG2,
∴PG=![]() =1,
=1,
∴PC=2PG=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(﹣2017)+2016的结果是( ).
A. ﹣4033 B. ﹣1 C. 1 D. 4033
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个多边行的边数增加,则它的外角和( )
A. 随着增加B. 保持不变C. 随着减少D. 无法确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABD和△ACE中,有下列四个等式:①AB=AC;②AD=AE;③∠1=∠2;④BD=CE.以其中三个条件为题设,填入已知栏中,一个论断为结论,填入下面求证栏中,使之组成一个真命题,并写出证明过程.
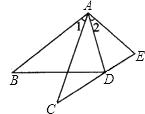
已知: .
求证: .
证明:
-
科目: 来源: 题型:
查看答案和解析>>【题目】小红和爷爷在400米环形跑道上跑步.他们从某处同时出发,如果同向而行,那么经过200 s小红追上爷爷;如果背向而行,那么经过40 s两人相遇,求他们的跑步速度.
(1)写出题目中的两个等量关系;
(2)给出上述问题的完整解答过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】据第二次全国经济普查资料修订及各项数据初步核算,岳阳市GDP从2007年的987.9亿元增加到2009年的1272.2亿元.设平均年增长率为x,则可列方程为.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形的内角和是外角和的2倍,则这个多边形的边数为( )
A.4
B.5
C.6
D.7
相关试题

