【题目】一袋中装有形状大小都相同的四个小球,每个小球上各标有一个数字,分别是1,4,7,8.现规定从袋中任取一个小球,对应的数字作为一个两位数的个位数;然后将小球放回袋中并搅拌均匀,再任取一个小球,对应的数字作为这个两位数的十位数.
(1)写出按上述规定得到所有可能的两位数;
(2)从这些两位数中任取一个,求其算术平方根大于4且小于7的概率.
【答案】(1)16种等可能的结果数,它们是:11,41,71,81,14,44,74,84,17,47,77,87,18,48,78,88;(2)![]()
【解析】(1)画树状图:

共有16种等可能的结果数,它们是:11,41,71,81,14,44,74,84,17,47,77,87,18,48,78,88;
(2)算术平方根大于4且小于7的结果数为6,
所以算术平方根大于4且小于7的概率=![]() =3/8.
=3/8.
【题型】解答题
【结束】
23
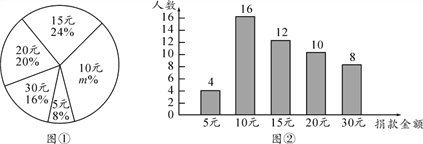
【题目】某高校学生会向全校2900名学生发起了“爱心一日捐”捐款活动,为了解捐款情况,学生会随机调查了部分学生的捐款金额,并用得到的数据绘制了如下统计图①和图②,请根据相关信息,解答下列问题:
(1)本次接受随机抽样调查的学生人数为____,图①中m的值是____;
(2)求本次你调查获取的样本数据的平均数、众数和中位数;
(3)根据样本数据,估计该校本次活动捐款金额为10元的学生人数.
参考答案:
【答案】(1)50,32;(2)平均数是16,众数是10元,中位数是15元; (3) 928人.
【解析】分析:(1)由捐5元的4人占调查人数的8%求调查的总人数;捐10元的人数除以调查的总人数可求m;(2)根据平均数,众数,中位数的定义求解;(3)用调查人数中捐10元的百分比乘以本校人数.
详解:(1)本次接受随机抽样调查的学生人数为4÷8%=50(人);
因为![]() ×100%=32%,所以m=32.
×100%=32%,所以m=32.
故答案为50,32;
(2)平均数是![]() (4×5+16×10+12×15+10×20+8×30)=16(元),
(4×5+16×10+12×15+10×20+8×30)=16(元),
众数是10元,中位数是15元.
(3)该校本次活动捐款金额为10元的学生人数是2900×32%=928(人)
-
科目: 来源: 题型:
查看答案和解析>>【题目】结合数轴与绝对值的知识回答下列问题:
(1)数轴上表示4和1的两点之间的距离是 ;表示-3和2两点之间的距离是 ;一般地,数轴上表示数m和数n的两点之间的距离等于
 .如果表示数
.如果表示数 和-2的两点之间的距离是3,那么
和-2的两点之间的距离是3,那么 = ;
= ;(2)若数轴上表示数
 的点位于-4与2之间,求
的点位于-4与2之间,求 +
+ 的值;
的值; -
科目: 来源: 题型:
查看答案和解析>>【题目】校医务人员对十名同学的身高进行检测,以150cm为标准,超过记作“+”,不足记为“-”,如:152cm记为+2cm,145cm记为-5cm,已知十名同学的身高记录如下:+4.5,-1.5,+4.5,-3.0,-2.4,+5.0,+8.2,-6.5,-7.2,+2.4,
(1)最高的同学身高为 cm,最矮的同学身高为 cm;
(2)求这十名同学的平均身高.
-
科目: 来源: 题型:
查看答案和解析>>【题目】星期五晚上,小明和他的妈妈一起看《歌手》,歌手演唱完后要评选出名次,在已公布四到七名后,还有华晨宇、汪峰、张韶涵三位选手没有公布名次.
(1)求汪峰获第一名的概率;
(2)如果小明和妈妈一起竞猜第一名,那么两人中一个人猜中另一个人却没猜中的概率是多少?(请用“树状图”或“列表”等方法写出分析过程)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,
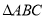 .
.(1)请以AB、BC为邻边用两种不同的方法画平行四边形ABCD,并说明此画法的合理性(不写作法,保留作图痕迹.);
(2)在上述画出的平行四边形中,若
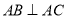 ,
,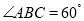 ,
,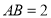 ,求对角线BD的长.
,求对角线BD的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】感知:如图(1),已知正方形ABCD和等腰直角△EBF,点E在正方形BC边上,点F在AB边的延长线上,∠EBF=90°,连结AE、CF.
易证:∠AEB=∠CFB(不需要证明).
探究:如图(2),已知正方形ABCD和等腰直角△EBF,点E在正方形ABCD内部,点F在正方形ABCD外部,∠EBF=90°,连结AE、CF.
求证:∠AEB=∠CFB
应用:如图(3),在(2)的条件下,当A、E、F三点共线时,连结CE,若AE=1,EF=2,则CE=______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市去年第一季度平均每月盈利2万元,第二季度平均每月亏损1.5万元,第三季度平均每月亏损1.7万元,第四季度平均每月盈利2.5万元.
(1)将盈利记为“+”,亏损记为“-”,补充下表:(单位:万元)

(2)这家超市去年总盈亏情况如何?
相关试题

