【题目】如图,在长方形ABCD中,AB=4,AD=6,延长BC到点E,使CE=2,连结DE,动点P从点B出发,以每秒2个单位的速度沿BC→CD→DA向终点A运动,设点P的运动时间为t(s),当t为何值时,△ABP和△DCE全等?

参考答案:
【答案】当t=1或7时,△ABP和△DCE全等
【解析】试题分析:由条件可以知道BP=2t,当点P在线段BC上时,可以知道BP=CE,当点P在线段DA上时,有AD=CE,分别可得到关于t的方程,可求得t的值.
试题解析:∵AB=CD,∠A=∠B=∠DCE=90°,
∴△ABP≌△DCE或△BAP≌△DCE.
当△ABP≌△DCE时,BP=CE=2,
此时2t=2,解得t=1.
当△BAP≌△DCE时,AP=CE=2,
此时BC+CD+DP=BC+CD+(DA-AP)=6+4+(6-2)=14,即2t=14,解得t=7.
∴当t=1或7时,△ABP和△DCE全等.
-
科目: 来源: 题型:
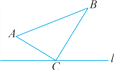
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,AC=6,BC=8.点P从点A出发沿路径A→C→B向终点B运动;点Q从点B出发沿路径B→C→A向终点A运动.点P和点Q分别以1个单位/秒和3个单位/秒的速度同时开始运动,两点都要到相应的终点时才能停止运动,在某一时刻,过点P作PE⊥l于点E,过点Q作QF⊥l于点F.问:点P运动多少时间时,△PEC与△CFQ全等?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】船在静水中的速度为a千米/时,水流速度为18千米/时,船顺水航行5小时的行程比船逆水航行4小时的行程多_________千米
-
科目: 来源: 题型:
查看答案和解析>>【题目】九年级某班同学在庆祝2015年元旦晚会上进行抽奖活动.在一个不透明的口袋中有三个完全相同的小球,把它们分别标号1、2、3.随机摸出一个小球记下标号后放回摇匀,再从中随机摸出一个小球记下标号.
(1)请用列表或画树形图的方法(只选其中一种),表示两次摸出小球上的标号的所有结果;
(2)规定当两次摸出的小球标号相同时中奖,求中奖的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个小球向斜上方抛出,它的行进高度y(单位:m)与水平距离x(单位:m)之间的关系是y=﹣x2+4x+1,则小球能到达的最大高度是m.
-
科目: 来源: 题型:
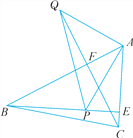
查看答案和解析>>【题目】如图,已知在△ABC中,AB>AC,BE,CF都是△ABC的高线,P是BE上一点,且BP=AC,Q是CF延长线上一点,且CQ=AB,连结AP,AQ,QP.求证:
(1)AQ=PA.
(2)AP⊥AQ.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a-b=2019,c+d=2018,则 (b+c)-(a-d ) 的值是___________
相关试题

