【题目】
![]()
(1)OA= cm,OB= cm.
(2)若点C是线段AO上一点,且满足AC=CO+CB,求CO的长.
(3)若动点P、Q分别从A、B同时出发,向右运动,点P的速度为2cm/s,点Q的速度为1cm/s,设运动时间为t(s),当点P与点Q重合时,P、Q两点停止运动.
①当t为何值时,2OP﹣OQ=8.
②当点P经过点O时,动点M从点O出发,以3cm/s的速度也向右运动.当点M追上点Q后立即返回,以同样的速度向点P运动,遇到点P后立即返回,又以同样的速度向点Q运动,如此往返,直到点P、Q停止时,点M也停止运动.在此过程中,点M行驶的总路程为 cm.
参考答案:
【答案】(1)16,8;(2)CO=![]() ;(3)①t=
;(3)①t=![]() 或16s时,2OP﹣OQ=8.②48cm.
或16s时,2OP﹣OQ=8.②48cm.
【解析】试题分析:(1)由OA=2OB,OA+OB=24即可求出OA、OB.
(2)设OC=x,则AC=16﹣x,BC=8+x,根据AC=CO+CB列出方程即可解决.
(3)①分两种情形①当点P在点O左边时,2(16﹣2t)﹣(8+t)=8,当点P在点O右边时,2(2t﹣16)﹣(8+x)=8,解方程即可.
②点M运动的时间就是点P从点O开始到追到点Q的时间,设点M运动的时间为ts由题意得:t(2﹣1)=16由此即可解决.
解:(1)∵AB=24,OA=2OB,
∴20B+OB=24,
∴OB=8,0A=16,
故答案分别为16,8.
(2)设CO=x,则AC=16﹣x,BC=8+x,
∵AC=CO+CB,
∴16﹣x=x+8+x,
∴x=![]() ,
,
∴CO=![]() .
.
(3)①当点P在点O左边时,2(16﹣2t)﹣(8+t)=8,t=![]() ,
,
当点P在点O右边时,2(2t﹣16)﹣(8+t)=8,t=16,
∴t=![]() 或16s时,2OP﹣OQ=8.
或16s时,2OP﹣OQ=8.
②设点M运动的时间为ts,由题意:t(2﹣1)=16,t=16,
∴点M运动的路程为16×3=48cm.
故答案为48cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个三角形三个内角度数的比为2︰7︰4,那么这个三角形是( )
A.直角三角形
B.锐角三角形
C.钝角三角形
D.等边三角形 -
科目: 来源: 题型:
查看答案和解析>>【题目】解方程2x+1=3(x﹣1).
-
科目: 来源: 题型:
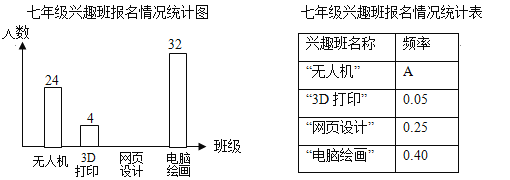
查看答案和解析>>【题目】学校计划在七年级学生中开设4个信息技术应用兴趣班,分别为“无人机”班,“3D打印”班,“网页设计”班,“电脑绘画”班,规定每人最多参加一个班,自愿报名.根据报名情况绘制了下面统计图表,请回答下列问题:
(1)报名参加兴趣班的总人数为 人;统计表中的A= ;
(2)将统计图补充完整;
(3)为了均衡班级人数,在“电脑绘画”班中至少动员几人到“3D打印”班,才能使“电脑绘画”班人数不超过“3D打印”班人数的2倍?
-
科目: 来源: 题型:
查看答案和解析>>【题目】三淅高速2015年建成通车,三门峡到南阳全长291.6千米,将291.6千米用科学记数法表示为( )
A.2.916×106米
B.2.916×105米
C.29.16×105米
D.2.916×104米 -
科目: 来源: 题型:
查看答案和解析>>【题目】小张在甲楼A处向外看,由于受到前面乙楼的遮挡,最近只能看到地面D处,俯角为α.小颖在甲楼B处(B在A的正下方)向外看,最近能看到地面E处,俯角为β,地面上G,F,D,E在同一直线上,已知乙楼高CF为10m,甲乙两楼相距FG为15m,俯角α=45,β=35.
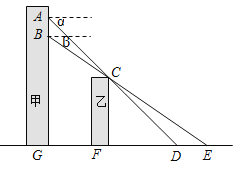
(1)求点A到地面的距离AG;
(2)求A,B之间的距离.(结果精确到0.1m)
(sin35≈0.57,cos35≈0.82,tan35≈0.70)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中正确的是 ( )
A. 变量 x , y 满足 x + 3y = 1 ,则 y 是 x 的函数
B. 变量 x , y 满足
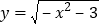 ,则 y 是 x 的函数
,则 y 是 x 的函数C. 变量 x , y 满足∣ y ∣= x ,则 y 是 x 的函数
D. 变量 x , y 满足 y2 = x ,则 y 是 x 的函数
相关试题

