【题目】小张在甲楼A处向外看,由于受到前面乙楼的遮挡,最近只能看到地面D处,俯角为α.小颖在甲楼B处(B在A的正下方)向外看,最近能看到地面E处,俯角为β,地面上G,F,D,E在同一直线上,已知乙楼高CF为10m,甲乙两楼相距FG为15m,俯角α=45,β=35.
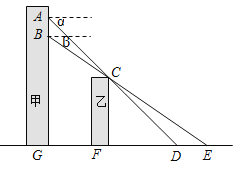
(1)求点A到地面的距离AG;
(2)求A,B之间的距离.(结果精确到0.1m)
(sin35≈0.57,cos35≈0.82,tan35≈0.70)
参考答案:
【答案】(1)位置A离地面的垂直距离为25米;
(2)A,B相差4.5米.
【解析】试题分析:(1)由题意可知∠AGD=∠BGE=∠CFD=900,∠CDF=α=45°,即可得DF=CF=10,DG=FG+FD=15+10=25,所以AG=GD=25;(2)在Rt△CEF中,根据∠CEF的正切可求得EF的长,即可得EG的长,在Rt△BGE中,根据∠CEF的正切可求得BG的长,即可求得AB的长.
试题解析:
(1)由已知得:∠AGD=∠BGE=∠CFD=900,∠CDF=α=450,
∴DF=CF=10,DG=FG+FD=15+10=25,
∴AG=GD=25,
答:位置A离地面的垂直距离为25米.
(2)∵∠CEF=β=350,
∴![]() tan∠CEF=tan350≈0.70,
tan∠CEF=tan350≈0.70,
∴EF=![]()
![]() ≈14.29,
≈14.29,
∴EG=GF+EF=15+14.29=29.29,
又∵![]() tan∠CEF=tan350≈0.70,
tan∠CEF=tan350≈0.70,
∴BG=0.70EG=0.70×29.29≈20.50,
∴AB≈25-20.50≈4.5.
答:A,B相差4.5米.
-
科目: 来源: 题型:
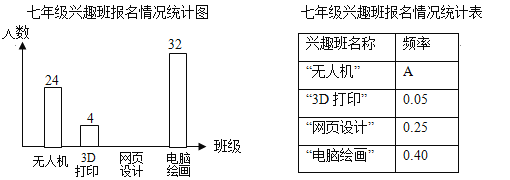
查看答案和解析>>【题目】学校计划在七年级学生中开设4个信息技术应用兴趣班,分别为“无人机”班,“3D打印”班,“网页设计”班,“电脑绘画”班,规定每人最多参加一个班,自愿报名.根据报名情况绘制了下面统计图表,请回答下列问题:
(1)报名参加兴趣班的总人数为 人;统计表中的A= ;
(2)将统计图补充完整;
(3)为了均衡班级人数,在“电脑绘画”班中至少动员几人到“3D打印”班,才能使“电脑绘画”班人数不超过“3D打印”班人数的2倍?
-
科目: 来源: 题型:
查看答案和解析>>【题目】

(1)OA= cm,OB= cm.
(2)若点C是线段AO上一点,且满足AC=CO+CB,求CO的长.
(3)若动点P、Q分别从A、B同时出发,向右运动,点P的速度为2cm/s,点Q的速度为1cm/s,设运动时间为t(s),当点P与点Q重合时,P、Q两点停止运动.
①当t为何值时,2OP﹣OQ=8.
②当点P经过点O时,动点M从点O出发,以3cm/s的速度也向右运动.当点M追上点Q后立即返回,以同样的速度向点P运动,遇到点P后立即返回,又以同样的速度向点Q运动,如此往返,直到点P、Q停止时,点M也停止运动.在此过程中,点M行驶的总路程为 cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】三淅高速2015年建成通车,三门峡到南阳全长291.6千米,将291.6千米用科学记数法表示为( )
A.2.916×106米
B.2.916×105米
C.29.16×105米
D.2.916×104米 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中正确的是 ( )
A. 变量 x , y 满足 x + 3y = 1 ,则 y 是 x 的函数
B. 变量 x , y 满足
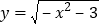 ,则 y 是 x 的函数
,则 y 是 x 的函数C. 变量 x , y 满足∣ y ∣= x ,则 y 是 x 的函数
D. 变量 x , y 满足 y2 = x ,则 y 是 x 的函数
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD为△ABC的中线,BE为三角形ABD中线,
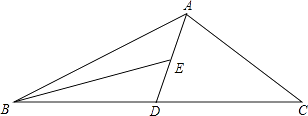
(1)∠ABE=15°,∠BAD=35°,求∠BED的度数;
(2)在△BED中作BD边上的高;
(3)若△ABC的面积为60,BD=5,则点E到BC边的距离为多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边△ABC中,M为BC边上的中点,D是射线AM上的一个动点,以CD为一边且在CD的下方作等边△CDE,连接BE.

(1)填空:若D与M重合时(如图1)∠CBE=度;
(2)如图2,当点D在线段AM上时(点D不与A、M重合),请判断(1)中结论是否成立?并说明理由;
(3)在(1)的条件下,若AB=6,试求CE的长.
相关试题

