Question

【题目】如图，在四边形ABCD中，AD∥BC，E是AB的中点，连接DE并延长交CB的延长线于点F，点M在BC边上，且∠MDF=∠ADF．

（1）求证：△ADE≌△BFE．

（2）连接EM，如果FM=DM，判断EM与DF的关系，并说明理由．

Answer 1

【答案】（1）证明见解析；（2）EM与DM的关系是EM垂直且平分DF；理由见解析.

【解析】试题分析：（1）由平行线的性质得出∠ADE=∠BFE，由E为AB的中点，得出AE=BE，由AAS证明△AED≌△BFE即可；

（2）由△AED≌△BFE，得出对应边相等DE=EF，证明FM=DM，由三角形的三线合一性质得出EM⊥DF，即可得出结论．

试题解析：（1）证明：∵AD∥BC，

∴∠ADE=∠BFE，

∵E为AB的中点，

∴AE=BE，

在△AED和△BFE中，

，

∴△AED≌△BFE（AAS）；

（2）解：EM与DM的关系是EM垂直且平分DF；理由如下：

连接EM，如图所示：

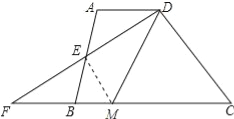
由（1）得：△AED≌△BFE，

∴DE=EF，

∵∠MDF=∠ADF，∠ADE=∠BFE，

∴∠MDF=∠BFE，

∴FM=DM，

∴EM⊥DF，

∴ME垂直平分DF．