【题目】东坡商贸公司购进某种水果的成本为20元/kg,经市场调研发现,这种水果在未来48天的销售价格p(元/kg)与时间t(天)之间的函数关系式为p=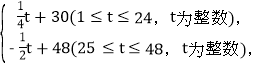 且日销售量y(kg)与销售时间t(天)的关系如下表:
且日销售量y(kg)与销售时间t(天)的关系如下表:

(1)已知y与t的变化规律符合一次函数关系,试求在第30天的日销售量是多少;
(2)问哪一天的销售利润最大,最大日销售利润为多少?
(3)在实际销售的前24天中,公司决定每销售1 kg水果就捐赠n元利润(n<9)给“精准扶贫”对象,现发现:在前24天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围.
参考答案:
【答案】(1)第30天的日销售量为60千克;(2)在第10天的销售利润最大,最大日销售利润为1 250元;(3)7≤n<9.
【解析】分析:(1)设y=kt+b,利用待定系数法即可解决问题.
(2)日利润=日销售量×每公斤利润,据此分别表示前24天和后24天的日利润,根据函数性质求最大值后比较得结论.
(3)列式表示前24天中每天扣除捐赠后的日销售利润,根据函数性质求n的取值范围.
详解:(1)设y=kt+b,把t=1,y=118;t=3,y=114代入得到:
![]() 解得
解得![]() ,
,
∴y=120-2t,
当t=30时,y=120-60=60.
即在第30天的日销售量为60千克.
(2)设日销售利润为w元,则w=(p-20)y.
当1≤t≤24时,w=![]() (120-2t)=-
(120-2t)=-![]() t2+10t+1 200=-
t2+10t+1 200=-![]() (t-10)2+1 250.
(t-10)2+1 250.
∴当t=10时,w最大=1 250.
当25≤t≤48时,w=![]() (120-2t)=t2-116t+3 360=(t-58)2-4,
(120-2t)=t2-116t+3 360=(t-58)2-4,
由二次函数的图象及性质知当t=25时,w最大=1 085.
∵1 250>1 085,
∴在第10天的销售利润最大,最大日销售利润为1 250元.
(3)设每天扣除捐赠后的日销售利润为w1元,
依题意得w1=![]() (120-2t).
(120-2t).
=-![]() t2+2(n+5)t+1 200-120n(1≤t≤24),
t2+2(n+5)t+1 200-120n(1≤t≤24),
其图象的对称轴为直线t=2n+10,
要使w1随t的增大而增大,
由二次函数的图象及性质知2n+10≥24,解得n≥7.
又∵n<9,∴7≤n<9.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“端午节”是我国的传统佳节,民间历来有吃“粽子”的习俗. 我市某食品厂为了解市民对去年销量较好的肉馅粽、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A、B、C、D表示)这四种不同口味粽子的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整). 请根据以上信息回答:
(1)本次参加抽样调查的居民有多少人?
(2)将两幅不完整的图补充完整;
(3)若居民区有8000人,请估计爱吃D粽的人数;

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图
 ,试判断
,试判断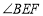 、
、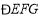 、
、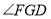 之间的关系.并说明理由.
之间的关系.并说明理由.(2)如图
 ,
, ,
, .试判断
.试判断 和
和 的位置关系,并说明理由.
的位置关系,并说明理由.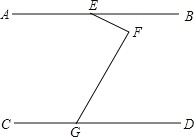
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据给出的数轴及已知条件,解答下面的问题:
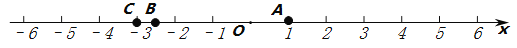
(1)已知点A,B,C表示的数分别为1,
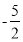 ,-3.观察数轴,与点A的距离为3的点表示的数是 ,A,B两点之间的距离为 。
,-3.观察数轴,与点A的距离为3的点表示的数是 ,A,B两点之间的距离为 。(2)数轴上,点B关于点A的对称点表示的数是 ;
(3)若将数轴折叠,使得A点与C点重合,则与B点重合的点表示的数是 ;若此数轴上M,N两点之间的距离为2019(M在N的左侧),且当A点与C点重合时,M点与N点也恰好重合,则点M表示的数是 ,点N表示的数是 。
(4)若数轴上P,Q两点间的距离为a(P在Q的左侧),表示数b的点到P,Q的两点的距离相等,将数轴折叠,当P点与Q点重合时,点P表示的数是 ,点Q表示的数是 (用含a,b的式子表示这两个数)。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为了解该校学生的课余活动情况,采用抽样调查的方式,从运动、娱乐、阅读和其他四个方面调查了若干名学生的兴趣和爱好情况,并根据调查结果制作了如下两幅统计图.

根据图中提供的信息解答下列问题:
(1)求本次抽样调查的人数;(要求列式计算,写出求解过程)
(2)补全人数统计图;
(3)“运动”对应的扇形的圆心角度数是 度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,每个小方格都是边长为
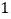 的正方形,
的正方形,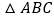 的顶点均在格点上,点
的顶点均在格点上,点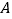 的坐标是
的坐标是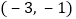 .
.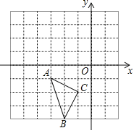
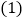 先将
先将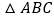 沿
沿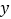 轴正方向向上平移
轴正方向向上平移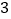 个单位长度,再沿
个单位长度,再沿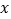 轴负方向向左平移
轴负方向向左平移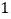 个单位长度得到
个单位长度得到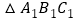 ,画出
,画出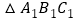 ,点
,点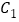 坐标是________;
坐标是________;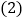 将
将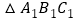 绕点
绕点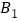 逆时针旋转
逆时针旋转 ,得到
,得到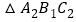 ,画出
,画出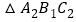 ,并求出点
,并求出点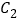 的坐标是________;
的坐标是________;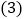 我们发现点
我们发现点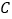 、
、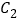 关于某点中心对称,对称中心的坐标是________.
关于某点中心对称,对称中心的坐标是________. -
科目: 来源: 题型:
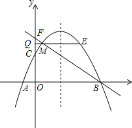
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴交于A(﹣1,0),B(4,0)两点,与y轴交于点C(0,2),点M(m,n)是抛物线上一动点,位于对称轴的左侧,并且不在坐标轴上,过点M作x轴的平行线交y轴于点Q,交抛物线于另一点E,直线BM交y轴于点F.
(1)求抛物线的解析式,并写出其顶点坐标;
(2)当S△MFQ:S△MEB=1:3时,求点M的坐标.
相关试题

